
I don't offer live buttons because I promised not to expose my visitors to surveillance through third-party scripting. To share a link, please click to select one. As it turned blue, right-click on it and pick "Copy" from the browser's menu. To insert the copied link wherever your like, right-click again and pick "Paste" from the browser's menu.
Close this link selector..
Only parent can teach.
Patent pending
© 2014 Georgiy Kuznetsov
In the beginning, I told how my first two American kids became math haters at schools. I failed to help the first one, and it hurts. When education kicked the second one off track, I managed to put her back. By the end of the fourth grade, she was the best in class. She brought home the "gold seal" for "educational excellence", what I did not want at all. Good thing though, she is not miserable at school any more.
I am working with my third and, probably, the last child to prevent another disaster.
DEFENSIVE MATH was a reluctant offspring of my two other projects: MAKE THEM MAD and SHNUMBERS. What started as early teaching and remediation, grew into defense.Many posts here are not sufficiently simple and detailed, but it's not a product yet. It only gives some idea what DEFENSIVE MATH could be like, if I'll get to finish it.
Once and for all, please excuse my English.
To call Table of Contents from anywhere at any time or to close it, please use the TOC control in the top-right corner. Thank you!
Next to the TOC there is the SHARE control. Click on it it to get the social media links.
The SIX opens the SIX PROJECTS web site. The DEFENSIVE MATH is one of them. Follow this link to find my email address.
The STEREO is the link to the online presentation STEREO LEARNING. It demonstrates how the projects work together to make STEM subjects learnable and their students teachable.
Clever Hans and Bright John
Seriously, how can they not understand that those Harlem Shake videos are metaphors of ejaculation? Are they pretending? OK, that's none of my business. I just wanted to check on so-called Internet memes, specifically on one of them, which states that multiplication is not repeated addition.
When I came across this idea, I thought that it belonged to Defensive Math. Yet, upon closer examination, I saw familiar logic, according to which fingers are for nose-picking. If multiplication is repeated addition, who needs school to teach it?
Soon I found that the meme was being promoted to educators, and it was gaining traction among them. Now, what is good for educators is rarely good for students. Defensive math is about defending students from teachers, not the other way around.
As a parent, I thought MINRA can be very damaging, and it could explains some peculiarities of elementary school teaching. Otherwise, I did not find MINRA apologetics remarkable, except the following point. Here is the link and the quote.
"Oh, so multiplication of fractions is a DIFFERENT kind of multiplication, is it?" a bright kid will say, wondering how many more times you are going to switch the rules. No wonder so many people end up thinking mathematics is just a bunch of arbitrary, illogical rules that cannot be figured out but simply have to be learned - only for them to have the rug pulled from under them when the rule they just learned is replaced by some other (seemingly) arbitrary, illogical rule.
Irony? Hardly. The author just wanted to make such bright kids happy.

Folklore has many tales of bright guys and the rugs pulled out from under their feet. The number in Aarne-Thompson classification is 1696 (The stupid man/What Should I Have Said?). Here is a collection, thank you professor Ashliman! The first one was retold by Brothers Grimm. They included another one in their book. It's named "Clever Hans". Ironically, of course.
Links are unreliable, so please allow me another quote from Wikipedia. It's short and more understandable, although, I suspect, is not free from mistakes. For example, why say "not much"? Or - from another story - why put a knife and how to put a goat in the pocket, unless it's a pocket goat? Was it a bag of some kind?
A long long time ago there lived a mother and her son. The son told the mother that he wanted to go out a traveling. The mother was very worried about it since they were very poor. The son told her that he would be fine, and he would always say "not much". One day on his travels, he passed by a group of fishermen while he was saying "not much". The fishermen could not catch any fish and were very angry at him. He asked them what he should be saying instead. They told him to say "Get it full". He continued to say "get it full, get it full" while he was traveling. Then he passed by a gallows when some prisoners were being hung. The executioner got angry and said, "so it is good to have more criminals?". The young man asked what he should be saying instead. The executioner told him to say "God, please have pity on the poor soul". Then he came across a group of knackers who were skinning a horse while he was saying "God, please have pity on the poor soul." The knackers got mad and told him to say "there lies the dead flesh in the pit". So the young man kept on traveling while he was saying "there lies the dead flesh in the pit." A cart passed by and fell into a pit. The people in the cart were mad and start attacking the young man. He ran back home and never went out a traveling again in his life.
The story is clearly not for a school library. The synopsis failed to mention that everybody ended up "attacking" the stupid one, hurting him pretty badly. I gave Brother Grimm's stories to TLG to read. Another reason to wait for police to knock on the door.
Comparing two quotes, I can't help but marveling at the cultural shift, which mass education induced in the last 250 years. Dumbing down to cater to imaginary masses they said? The tales collected by Brothers Grimm were not exactly pinnacles of intellectuality, but their Clever Hans is now our Bright John.
I wonder what even moderately dim student would fail to understand that math is a developing knowledge, and when you learn math, it develops in your mind. They tell you one-two-three-four-five-six-seven-eight-nine-ten are numbers. Then you have to go to 20. And zero. And -1. And fractions... and now I feel like the rug is pulling my feet. Why, why, why do they say that multiplication of fractions is not the same multiplication, which has been known for millenia?
I can't speak for the masses. They can be this stupid, of course. I can also tell that the masses are being taught precisely this kind of mechanically separated math, in which nothing makes sense even for the teachers. Another factor is obvious too: stupid students are good for the schools. First, the teachers themselves don't have to be smart. Then, nobody can expect and demand the stupid students to learn much of anything. US educators grew very good at picturing their students as stupid, making them stupid and silencing those who don't accept this role.
By the way, the first quotation only makes sense if Bright John will live to learn true math. This is then the false knowledge of multiplication as repeated addition will return to bite his butt.
What does it take to multiply?
Two weeks ago me and my still-6-year-old student TLG started practicing multiplication on an industrial scale. Her current throughput is one 5x5 operation in 20 minutes, and she is improving. She is also learning to troubleshoot her computations and fix mistakes,
Please don't think I am about to teach you multiplication. I am just going to remind you what it takes.
TLG has known multiplication and division since she was 4, but it was not in positional notations. Understanding positional multiplication took her 2 years of my lazy lessons. Not all of them of course, and not even the biggest part of them.
After the initial spatiotemporal training, she learned positional addition in shnumbers. Then she went to numerals working (mostly) with random 10-digit numbers and using the charts of her own making. She learned addition "facts" while adding. Unfortunately, I did not count those 10-digit additions. Looks like she performed less than 30 of them.
According to my homegrown strategy, multiplication teaches addition much better than addition teaches itself. The same is true for long additions teaching one-digit additions.
More than a year ago, TLG had created her first "times table". Sure enough, she filled it out using repeated additions.
TLG has learned exponentiation and developed rudimentary exponential thinking. Not only decimal, and I regularly expose her to non-decimal arithmetic.
I spent couple week's lessons playing with the elements of combinatorics. TLG may even remember factorial.
TLG is not really keen to study math, but she has the right attitude. As soon as she learned to understand my English, I kept telling her: we don't need these patterns, we build them because they are hard to build. She wouldn't run where she is supposed to swim. She only uses the calculator to verify her solutions. She even finds building 10 or 11 digit numbers by hand somewhat exciting.
TLG understood distributivity and remembers it well. In anything remotely similar to an alphabet, she could do transformations like
(A1 + A2)×M = A1×M + A2×M,
or
(A1 + A2)×(B1 + B2) = (A1 + A2)×B1 + (A1 + A2)×B2
= A1×B1 + A2×B1 + A1×B2 + A2×B2
or instantly
(A + B)×(E + F + G) = AE + AF + AG + BE + BF + BG
TLG knows that
NM×NK = NM+K
I'll check on her tomorrow to make sure she still does. She knew how to derive this identity anyway.
TLG knows that positional number means addition of multiplications of powers. She is fairly comfortable with
12345 = 1×104 + 2×103 + 3×102 + 4×101 + 5×100
Powers of the base are much easier to use than 1s with 0s.
Hence, TLG can take apart two long numbers and multiply them piece-by-piece using distributivity. She can do it in a single line or make a chart matching everything to everything else. Either way, multiplying N-digit number by M-digit number produces N×N partial multiplications, and to "add together" she must rewrite them into a long column.
Approaching the standard algorithm, TLG learned to twist a partial multiplication into a single line. The biggest challenge was to add the carry, and only then to write out the result. Granted, since her early spatiotemporal training, TLG has been very good at such things.
Accumulating or adding together five or more partial additions was easy. We practiced adding and subtracting several long numbers at once.
Trying to teach TLG the standard method of long multiplication, I found several problems. The biggest one was that her handwriting was still too clumsy for small digits. She now starts every multiplication from "setting the stage". This preparatory part on the picture is blue.
On such a stage, TLG has enough room for regular size carries. By the way, we use only 1/2" graph paper. We don't need photocopied forms.
TLG strikes through the carries to get them out of her way when she adds the partial multiplications. I tried several ways to indicate the starting positions and decided to use 0s, but not before TLG has learned to multiply on the Odhner's machine to verify her computations.
I don't care if multiplication is good math or if it's math at all. I accept that TLG may never in her life need to multiply two numbers, and she may forget everything in the next few months. Surely, school will work hard to push her back to the standards of mental developments.
Multiplication for me is a moral and an intellectual challenge. What else in elementary education can match complexity, sophistication and thrill of arithmetic? What can have such an impact on building a character? A child who learned it became a different person.
Geometry—who needs it today? Take it away, and kids will never have a chance to taste a theory.
Why educators hate counting?

The picture is from "The Book of Trades". It was created by Jost Amman and published in 1568.
One of the first observations I made trying to understand US elementary school was that the teachers not only sow and nurture what they were told was right - they aggressively prosecute and eradicate what they were told was wrong. Their major enemy is dactylonomy or finger reckoning.
For this column, I picked a recent article from The Atlantic. The authors try to convince educators to change their attitude. No doubt, school will not listen.
I made several half-hearted attempts to find out exactly when and how finger reckoning became so unwelcome. During antiquity and in the Middle ages it was perfectly fine. It fell out of grace somewhere between 15th and 20th centuries AD.
The obvious reason for expelling finger reckoning from classrooms could be the raise of the Hindu-Arabic numeral system, which we use today. Popularly, it's importation is credited to Leonardo Fibonacci. Apparently, long before him, the wizards of Europe were reading the Latin translations of the works of Muhammad ibn Musa al-Khwarizmi and wondering who could have written them.
Like book printing, the Hindu-Arabic system became popular due to an unsung innovation: Europeans had learned Chinese art of paper making. I heard they started producing paper because they were drowning under rags, and the reason they suddenly faced such an abundance of linen and hemp was the plague.
The next critical change occurred only in 1840s. Industrialists in Germany and Canada learned to make paper out of wood pulp. Their product quickly became cheap enough for disposable news, but schools at that time and well into the 20th century were using even cheaper substitute: slates.
Their numeracy was about traditional units of money and measurement. Only the numerals were decimal. The technology, however, was modern because calculations were performed in writing. Before writable arithmetic, people had to rely on their fingers and abaci.
The modern school was quite new back then. The king of Prussia Friedrich the Great kick-started the famous Prussian education system in 1763, but only after Napoleonic Wars Europeans took mass education seriously. Napoleon, by the way, promoted decimalisation.
The man behing the Prussian reform was Johann Julius Hecker. He could have been the first to teach teachers. Wikipedia says that the Prussian system "was adopted by all American K-12 public schools and major universities as early as the late 18th century". Did Hecker's seminary teach teachers to root out finger reckoning?By the middle of the 19th century, elementary education was becoming mandatory. Could this entice educators to crack down on out-of-school knowledge to solidify their emerging monopoly?
Literacy and numeracy, dilapidating cornerstones of US elementary school, are inextricably tied to paper. Even teaching reading using computers, they teach to read from paper. Apparently, at some moment, the teachers decried the shnumber methods and devices like calculi, fingers and abaci to concentrate on selling the only truly scientific technology. Whatever benefits for themselves they saw in it, they cling to paper, pencils and erasers even today, when devices made such a spectacular comeback.
From my American kids, I learned that the teachers secretly told them to use a number line if they can't remember a "math fact". I suspect this device is allowed due to the reasons discussed in this post. School favors stakes: They are more difficult to understand and to use. Devices use sticks. It is unlikely that this school will relearn arithmetic from devices anytime soon. Meanwhile, it's students live in the age of machine computations.
You may think that calculi, fingers, abaci and mechanical calculators were left in the dust. Well, so am I. I use calculi to teach quantity and even algorithms. My and my students' fingers are always with us. The method of positional addition in SHNUMBERS was adapted from decimal abaci, and it does teach numeracy, while elementary school scares students off it. Our Original-Odhner is indispensable for learning multiplication.
Outdated is the whole idea of arithmetic as of elementary math. Outside of schools, this business is called computing.
Meanwhile, paper teachers are struggling with silicon.
Way to go.
Before I forgot, the word algorithm is obviously Arabic, but only recently I learned that it's the name of al-Khwarizmi. The post stamp on the right is Soviet. Al-Khwarizmi was born in Khwarezm, in Uzbekistan, which was a part of USSR.
I started thinking about teaching TLG algorithms thanks to Steven Leinwand. My first reaction was, come on, you guys can't even explain multiplication. Eventually, I decided it was worth trying, and tried.
The material for TLG's first algorithm was bare quantity. I believe, the study of quantity must come before numeracy, and, since numeracy tends to erode the prior knowledge, we must reteach the fundamentals as often as possible.
Quantity is a property of sets of objects. We can't see it (which is truly remarkable). We discover it mentally.
Quantity is something that the sets of countable objects have in common, no matter how different those objects are. I provided some explanation in SHNUMBERS. Now I suspect I will never have a chance to tell everything I want, so please allow me to write just a little bit more.
As counting tokens, calculi or pebbles are second to none. They are small, dirt cheap, low maintenance, rock solid, stone durable, they can be easily differentiated by colors and shapes and even painted. Sadly, people waste plastics buying counting bears, cubes, beads.
As soon as we understood that we can match pebbles to hurricanes one by one and find the number of the pebbles bigger, we are on the way to math. The first step, I believe, is to learn to compare quantities.
I gave TLG two quantities in the paper bags, added one more empty bag, and challenged her to compare without taking all the tokens out. She was upset at first, but quickly understood the she only needed to match two tokens at a time. After she found which quantity was bigger, I started drafting the flowchart. Instantly, TLG learned the language and finished the story.

There is a problem with flowcharts. Let me borrow a piece from CODEPEGS to tell what it is.
Long time ago, when computer programming was in its infancy, we had statements allowing to leap back or forth and continue execution from any point. In 1968 a prominent Mufti named Edsger Wybe Dijkstra published a fatwa, in which he claimed that such statements are evil, and "should be abolished". So abolished they were.
Flowcharts allow to direct the flow of control to any point, so abolished they must be. I did not question the wisdom behind this decision and/or the outcome of it. I simply admit that recently I taught my 6 years 10 months old offspring use three kinds of blocks and lines with arrows to describe algorithms. Moreover, I am going to use flowcharts reteaching her every algorithm she has learned this far (and she is quickly approaching long division).
Three years ago, TLG underwent a course of procedural thinking. Back then, I did not understand what I was teaching her, and how this teaching was linked to my homegrown course of arithmetic. Only recently, I borrowed the unifying concept of spatiotemporal patterns.
Edsger Dijkstra wrote: "My second remark is that our intellectual powers are rather geared to master static relations and that our powers to visualize processes evolving in time are relatively poorly developed."
The "processes evolving in time" are spatiotermporal patterns, and they emerge from the procedures as we play them out. This was what TLG learned by the age of four.
Here is a very basic "checkerboard" pattern, which I temporalized in 6 different ways. I did it using FIREPEGS, which mimics much younger child. A year later the same child would build the same patterns procedurally.
What's next? I already have CODEPEGS. Soon (if not already) TLG may become able to build the patterns through JavaScript.
Are they addition?
 The mystery "add together" operation is known to Wikipedians as summation. You may even see this link on the "Multiplication" page. Well, multiplication is summation of the same number. Why don't they explain it this way?
The mystery "add together" operation is known to Wikipedians as summation. You may even see this link on the "Multiplication" page. Well, multiplication is summation of the same number. Why don't they explain it this way?
Summation according to Wikipedia to me is no less weird than multiplication. Looks like the writers were struggling with another instance of the "stick and stake" dilemma.
Addition is a binary operation and it involves two stakes. The number of additions is always 1 less than the number of the addends. Wikipedians are trying to avoid instructions like: skip 1, add any two numbers and count 2, add a new number to their sum and count 3... messy, indeed.
There is an obvious solution: begin adding from 0 and count from 1. In
0 + 4 + 4 + 4
the number of the + signs is equal to the number of the 4s. Why don't they teach this way?
Please start Windows Calculator (I believe, any other calculator will do) and type +4. It becomes 0+4. Now press "=" three times and get 12.
Windows Calculator and the similar devices (including the earliest mechanical calculators and my Original-Odhner) are accumulator machines. You got to clean (or zero) the accumulator before starting using it, so chains of additions start from 0.
In positional notation we omit the leading and the trailing zeros, but we remember they are here. For example,
1 +100
we understand as
001 +100
Similarly,
7 *100
is actually
7.00 *100.
and we move the point to make 700.
Can we understand
+N
as
0 +N
and
-N
as
0 -N?
If we could, we could consider addition of three 4s as increment by 4 three times. It might look like
+4 +4 +4
and sound like add four, add four, add four.
By the way,
0 -N
is negation, or just -N.
Is it strange to add without knowing the augend? To understand how it is possible, consider a simple positional shnumber machine presented in STEREOLEARNING. Click the FORWARD control in the bottom right corner to follow the explanation. A mechanical calculator is simply more complex (and much simpler to use).
By the way, like with any simple calculator, in SHNUMBERS we clean up the board and explicitly add the first quantity to 0. If empty spots and sheets of paper mean 0, we may think we add the first number by writing it. Are they teaching this at schools?
The odometer described by the Roman writer Vitruvius was supposed to count the distances dropping the pebbles in the accumulator bucket. One may imagine dropping several pebbles at a time. To accumulate those pebbles (or calculi), there was absolutely no need to know how many pebbles already were in the bucket. This was true addition.
I wonder why the engineers of Antiquity used the pebbles at all. Why didn't they draw the numbers on the wheel and take the readings? Was it easier to bring the bucket to the masons and order "this many" milestones?
The shnumber devices like abaci and calculators do use the augends. In a sense, they discover them while adding. The reason is: this devices receive the inputs and return results using numerals and/or positional notations.
Teaching unorthodox notations like
+4 +4 +4
is not a wise policy for a parent, but I have a story to tell. 3 years ago I was not sure how to teach TLG's big sister long multiplication. I didn't see much problems with teaching it, I just wanted to train her in a method endorsed by the educators in her country. It seemed that educators in the US were not endorsing any method and abandoned any hope to teach multiplication at all.
Eventually, I used a periodic discount to buy the video course "Mastering The Fundamentals of Mathematics" by professor James A. Sellers. I did not know US universities teach elementary math. It turned out, they do, and they do know multiplication.
My biggest concern was how to add the partial multiplications. I did not remember what they taught us at school, but I suspected in the US they were doing it differently. The writing media in my school were dip pens (complete with portable inkwells, believe it or not). US schools were relying on pencils and erasers.
I learned a lot from that video course. First of all, professor Seller told me that fifteen times three is fifteen three times. Then, to my astonishment, I realized that he was using pencil and eraser like any elementary school teacher. He was writing the carries in the same place, on top of the numbers. I could not believe they didn't let the students to keep track of their mistakes.
The biggest of his multiplications was 3x3 (456x123). When it came to adding 3 "long" numbers, I was holding my breath. OK, said professor, I taught you guys this stuff in my first lecture about addition.
He only taught addition of 2 long numbers. I had to assume that adding 3 long numbers at once was not in his curriculum at all.
Last Autumn, when I asked TLG to do long addition, she said she wanted to add 3 numbers. I muttered that three numbers are two numbers plus one, and only then I clicked. Adding "together" five or six long numbers, position by position, in accumulator mode: Yes, I did practice this. It was 51 or 52 years ago. So much progress in such a short time.
I picked two 10-digit numbers from TLG's stock and multiplied them by hand. My calculation is in the beginning of this page. I found only one acceptable way to keep track of the carries, and I suspect I would have done better with a dip pen. I simply did not have it. I used a ballpoint pen.
A mystery ghost operation spotted.
US education is practically impossible to discuss. For years, I was trying to figure out how schools teach multiplication. This helped me understand how to defend the kids from their teaching, but not to explain why do I think I have to defend them. The past observations worth nothing. Next time there will be another school, another teacher and another curriculum. The damage will be done, and only then I will have the valid reasons for defense.
That's why I am going to quote Wikipedia. To preserve their formatting, I captured the following from my browser's window.

My first question is: how multiplication can be defined as elementary if it is made of additions? Next, to put it gently, "may be thought as" is not a definition.
US schoolkids are being trained to add using math facts. The statements or expressions like "adding as many copies of them" immediately raises a question: adding to what?
The example of multiplying 3 by 4 in the following sentence makes the writers change the words: just "adding" becomes "adding together". I wonder if they actually teach an operation of "adding together". The reason is clear: they claim they add 3 times, but there are only 2 additions. Addition was not working for them. They tried to conjure up something else.
In my engineering view, those "elementary" operations exist only in teachers' imagination. Under the cover of arithmetic, we actually deal with 1s. To add means exactly to bring two sets of 1s together. Positional addition is only a method to handle big quantities of 1s quickly and easily.
Another remarkable aspect of this "definition" is the use of the notion of copying. Copying would make sense for quantities but not for numbers, unless the writers meant photocopying those numbers. A copy of a number is the same number. In multiplication we add the same numbers, not the copies of them.
I have no way to prove where those "copies" came from, but I suspect that they are creations of teachers' guilty conscience. The educators must understand that their elementary operation of multiplication is performing an impossible trick producing the quantities out of thin air. You have 4 dollars and you need more of them. Multiply by 3, and you have 12. "Copying" may be the teacher's way to explain how this can be possible. You just make the copies of your dollars.
The musing about "not very meaningful" distinction between the order of the multiplier and the multiplicand is superb. No, I have no mercy for the people who teach innocent children this stuff. Fortunately, they don't need my mercy.
A toy from the past.

Education is famously retarded. Schools always teach the citizens of tomorrow using yesterday's technologies. Not sure about this particular case, but usually they blame their retardations on the kids.
Interestingly, some tools of the past make very desirable and educating toys, if only they were explicitly repurposed. Teaching riding a horse instead of driving a car would not do much good, but how about a pet horse?
Here lies the problem. The tools of the past usually do not fit the economy of toys. I am trying to teach TLG vector graphics. A toy plotter would be great to have. Some are still available, and the used ones on eBay are not very expensive. I doubt if any of them accept SVG (how about Logo?), not to mention the interface, the driver and the supplies.
If anybody would take a risk to design such a toy and put it on the market, it would probably be too expensive. A toy is a one-time thing. Two times, maybe. The lesson will be learned quickly.
Several years ago I paid close to $300 for a well used Odhner Arithmometer on eBay. After some cleaning and oiling, it works acceptably well. Not sure if I would buy it again, but I am glad that once I did it.
The Odhner Atithmometer was a desktop mechanical calculator. Wikipedia has an article on it. Mine is newer than anything pictured there: The model number is 227.
At school, they gave us a brief course of using Arithmometer, and I did not quite get it. I recalled it when I was trying to teach TLG's big brother multiplication. It was hard, and suddenly I wished I had an Odhner.
It turned out, the Odhners were not common it the US and hard to come by. The idea was haunting me though. I finally got one when I started teaching TLG' big sister. By that time I knew why I wanted it. The Odhner Arithmometer was a shumber machine. Even my counting apps from SHNUMBERS had a similar interface.
As a pet, the Odhner Arithmometer has many nice features. For example, subtracting 35 from 0 it returns 9999999999965. Unfortunately, this little thing weights 12 lbs, so using it requires my constant supervision.
How a device covered in numbers can be a shnumber machine? Remember, my boards are marked with numbers too. Shnumbers embody quantity. Numbers symbolize it. Mechanical calculators like Odhner's don't use "math facts". The quantities are built in the pinwheels.
The Odhner Arithmometer is great for learning because to multiply a number on the cursors (levers) by N, one have to rotate the crank handle exactly N times (I wish every child would do it to understand what "number crunching" means). Isn't it how it should be? It is, but it isn't. I'll take a closer look next time.
Sorry, another big scare.
The British edition of Huffington Post reported an Internet sensation. I feel free to quote because the article mostly quotes the sources. Here it is, complete with the headline.
Year 2 SATs: Maths Question Aimed At Six And Seven-Year-Olds Is Completely Stumping Parents
Parents are claiming it’s too hard for their kids.
Parents are puzzled over a maths question that is aimed at Year 2 pupils taking their SATs exams.
Mum Louise Bloxham tweeted a photo of the task that involved working out how many people were on a train.
The question states: “There were some people on a train. 19 people get off the train at the first stop. 17 people get on the train.
“Now there are 63 people on the train. How many people were on the train to begin with?”
I gave the problem to TLG. In the middle of her 7th year, she is not a British 2nd year student of math, she is an American kindergartener learning to count to 20. Immediately, she started subtracting 17 from 63. Then she added 19. She messed up the computations - OK, there were the reasons for this - but her thinking was correct.
The parents' tweets quoted by HuffPost drew a familiar picture. In the age of free mandatory education, the majority of citizen perceive learning as a punishment. They hate school, then math, then - and most of all - algebra. How dare they ask our kiddies an algebra question?
No doubt, school is reaping what it sow, and it could not care less. Mandatory (or, more correctly, compulsory) education is a monopoly run on artificial sweeteners and fear.
Yet there is a math lesson in this story. Everybody assumed that the problem required equation, and equation is much-loathed algebra.
I had mentioned several times in this blog that I do not teach TLG equations. She simply knows how to solve them because she learned the operations of increment and decrement using X-bag.
Unlike addition and subtraction, increment and decrement are reversible, and not only conceptually so. I taught TLG the fully reversible algorithm of addition of shnumbers, on which she built her numerical carrying and borrowing skills.
Once TLG had gotten the problem, she started reversing the operations. This understanding was woven into the fabric of her mental arithmetic.
Increment and decrement are very useful for teaching. I will invoke them again and again.
The common method of teaching arithmetic is demotivating and debilitating. Guess, when schools will be allowed to teach children to walk, they will do it one step a year. I'll probably live to see how exciting it will be.
Not being able to stand the educational misery, I taught several first graders long numbers and addition. I was afraid to do it in the US, so I allowed the American school to make a math hater out of my oldest American child. With my second American child I did it again, and it helped.
The second child was seriously distressed. Looking for the least traumatic method, I borrowed a toy from my lessons with her little sister — the one I call the little girl or TLG. The toy worked surprisingly well, and soon I became using it to teach a four years old elementary math.
I am not an ambitious parent, and I had other things to do. I just fell into path dependence. I started playing with TLG when she was learning to speak. I had to keep teaching her after she turned four. My experience with her toy and her big sister suggested the most obvious way to go.
With TLG, my messy DYI teaching grew into a solid method. I started telling this story in SHNUMBERS, but found it too long for a demo. Eventually, I created STEREO LEARNING to tell it through animation.
The algorithms of long positional counting and addition shown in STEREO LEARNIG are standard for decimal counting frames. Every American school and many families have them and think they are just toys.
Like all abaci, the decimal counting frames gave rise to extremely popular and robust information technology. They coexisted with calculations on paper and easily outlived mechanical calculators. I suspect, in some countries people still use them.
For several important reasons, I would not rely on counting frames for teaching young kids positional arithmetic. Fortunately, I realized that another very common toy - a pegboard - could do the job much better.
With TLG's big sister, I did not pay attention to numeral words and phrases. I thought they were more English than math. TLG wanted to learn them and enjoyed this knowledge. To her it was empowering.
It so happened that, by the time TLG entered preschool, she could name and handle billions and trillions. She did not remember the bigger names. Neither did I.
With two American schoolchildren at home, I had to learn a thing or two about American education. I knew that cognitive development of young Americans was standardized in several contradicting ways, and that school was enforcing conformity to the standards. Understandably, teachers were not very eager to pull forward the students who were falling behind. With TLG I learned that teachers were very good at smothering the knowledge that should not be there.
Once TLG came home from preschool and proudly told me that she learned to count to 20. I asked her if she could count to anything bigger. She said she could not. I asked her what number goes after 20. She said it's 21, took a pencil and happily added up two 10 digits numbers. She loved doing this too.
I did not pay attention until this happened again. And again.
TLG's narratives were becoming elaborate. I talked to her, demonstrated to her her abilities and asked her to remember that she could count to any number. Sadly, I started noticing her emerging fear of big quantities.
Once again, TLG came home and told me that she knew how to count to 40. She said her big sister - a third grader as far as I remember - was allowed to count to one thousand, and her big brother must be able to count to one million.
The power of American educators appeared unsurmountable. I could not believe how easily they manipulated TLG. I talked to her again, very bluntly. Hadn't I done this, America would win another standard mind.
Miraculously, TLG understood that school was not teaching and should not be taken seriously. From time to time, I ask her what is the biggest number she can count to. She confirms that there is no limit to counting.
I wish I could tell that TLG is now free from fear. In the background, the school keeps doing its job. The next teacher is coming up soon. From time to time, I have to remind TLG that usually the bigger numbers are just more of the same.
I've seen four American preschools. Two of them were private and pretty benign. LIke, you know, we are not a garage daycare, he rent the premises, we hire the teachers, we are an academy, no less. Pay us more. We teach your children colors and shapes. Where else can they learn them? Not that I cared about colors and shapes, but I wanted my Russian kids to grow Americans.
TLG had attended two preschools closely affiliated with the local elementary school, and they were different. Apparently, they were charged with supplying standardized human material, and it was worse than I thought. Only the kindergarten started teaching the numbers to 20.
Talking to Kids
Watching the victims of education as a parent and remembering me being one of them, I realized that transition from arithmetic to algebra (as a school subject) is greatly complicated by the equal sign. If educators had any interest in learning, they would have never done such thing.
Elementary education teaches children that = means "go figure". Electronic calculator designers carved this meaning in plastic.
My last student, the little girl TLG, is a kindergartener and a native American English speaker. Five days a week, I hear her saying thing like
(a1 + a2)×M
equals
a1×M + a2×M
Not being a native American English speaker and a kindergartener, I always say is equal to.
I don't correct TLG because I want her to pass for a local at school. Wait a moment… thank you! I just checked with the online dictionaries. Only Cambridge explicitly had the elementary school meaning. The other five allowed to choose between "to be equal to" and "to make or produce something equal to". Well, as long as TLG uses the first definition where appropriate (and I see she does), her English is OK.
Mathematical expressions are stronger than words. Looking up online resources for first graders, I found tons of single digit additions in the classical form:
7 + 5 =If = means "is equal to", they make no sense because 7+5 is not equal to nothing.
At home, TLG has never practiced single digit additions. A true stereo learner, she learned long addition first, and started adding 10 digit numbers in standard decimal Hindu-Arabic notation before she turned five. Yet I've seen the damage caused by "go figure" meaning in every kid I taught before.
Instructions like "find a mystery number X such that X=7+5" would be better, but if we want them to add, why don't we just say "add this numbers"? And let the student answer: =12. I think, the sum is equal to 12.
Many websites are using columnar notation for single digit additions. This might help to pass the tests. Have you seen this method elsewhere?
The equal sign was introduced by Welsh mathematician and the first British algebraist Robert Recorde in his book The Whetstone of Witte published in 1557. Recorde stated his intentions very clearly: He was going to use = instead of writing "is equal to" every time. Before Recorde, people were using a different shorthand.
Equality is a relation. I prefer to explain it as a statement, which, like any statement, can be true or false. "Is equal to" really means "are equal" because if a=b then b=a.
Talking to Machines
Learning the artificial languages created to tell computers what to do, children face new challenges. Instead of familiar "go figure", in computer programming they find assignment.
Using a simple calculator, we press = key without thinking where the figured out value must go. It always goes to the display (which means, to its memory, because the display only shows what its memory holds).
In computers, the value goes to memory. It's huge and invisible, but numbered. To keep it manageable, computer programmers use variable names. Naming places in memory is a service, which every programming language offers nowadays. They maintain a table of variable names and memory locations.
Assignment makes the value in memory available through a variable name. In programing language, you may see:
a = 7
Which means, assign 7 to the variable name a (or make it point to 7).
Then the value of 5 may be assigned to the variable name b
b = 5
The third variable name c may receive the value of 12
c = a + b
How? OK, computer will replace the variable names with the values assigned to them and calculate the sum. In other words, the right side of so-called assignment is "go figure", scientifically known as evaluation.
Roughly speaking, there are two kinds of programming languages: one for the egg-heads, another one for those who learned their math in elementary school. The second kind is prospering.
You can instantly tell the languages of the second kind because they use = for assignment. Obviously, their creators wanted to be elementary school friendly, but they scare fellow graduates off talking about assignment instead of familiar "go figure".
Elementary school friendly computer languages do have the ways to express "is equal to". Usually it's == (two equal signs one after another). The trouble is, they treat them as questions. Expression like
a == b
are getting evaluated on par with arithmetical expressions. Computer languages answer the questions with boolean values true or false. Some even understand === for more specific purposes. Well, Robert Recorde drew his equal sign many times longer than we do today.
This leads me to Boolean algebra, but I am not going to follow. Boolean algebra is very accessible - a child of any age can understand the basics - and very useful. It fakes our thinking and makes it better. It's just a different topic.
Are Kids Machines?
When elementary school students meet variables, they demand the numerical values, and it's not out of stupidity. Kids simply do what they were trained to do. They said "go figure", but I need the figures for this!
Remarkably, that's how the general purpose programming languages react to variables names with no values to substitute. A program handling your input can ruthlessly points out that the variable is unknown, or its value have never been assigned.
Elementary school teaches human kids to act like simple computer programs, but kids have human emotions and attitudes. Algebra makes them suffer. Mandatory education does not care about students' sufferings. The business flourishes on their tears.
A teaching parent can easily prevent and counter such computerization. It's utterly important not to keep kids on steady diet of numbers. Young children, who learn to name things, easily pick up the idea of a variable. Optionally, it can be introduced through colors. From time to time, your student will scold you for teaching the stuff that normal American kids are not allowed to learn. Be prepared and don't give in.
Teaching, especially teaching a developing brain, is not enough. Every useful piece of knowledge must be maintained, and variables are very useful. Nine months ago, I went through a very difficult period. TLG got a live bird, and she forgot long subtraction. I re-taught it as a part of her mechanical "go figure" skills, but then I wanted her to learn to use it. Suppose you ate 223 candies out of 545. How many are left? No clue.
As usual, generalization helped. I told her that every known addition implies two other additions. If we know that any of the following statements is true, the other two are true too:
c = a + b b = c - a a = c - b
She knew this for years - for two years at least - but only with small numbers. Understandably, this informal knowledge was not even scalable. When she understood the abstract pattern, she started solving the problems with big numbers and without numbers at all.
Teaching equations wold be too distractive. I only wanted TLG to learn and remember how the quantities are related. Here they are in the stick notation:
Next are the stakes:
Soon TLG performed one of her routine long subtraction:
4456028506 -3548862305 907166201
I asked how she could verify the result. She said she could add the third number to the second. This was not new. I asked how else she could do it. To my astonishment, she suggested to subtract the third number from the first. With 10 digit, she could only infer this from the rules.
It was encouraging, but not enough to pass for a human by modern standards. Computer programs can do such things and more. Still, with "go figure" even such reasoning would be impossible. If I told a "go figure" student that
c = a + b
she or he would rightfully ask me what a and b were equal to… what I am talking about: It's not a columnar notation.
In 1st grade, the teacher caught TLG's big sister doing long addition. She learned the lesson, and did not reveal her ability to do long subtraction and multiplication prematurely. In 2nd grade, however, she was caught verifying small subtractions with additions. To her, it was natural because at home she used the chart of addition both ways. I quizzed her: What's five plus seven? Twelve minus five? Seven plus five? Five minus seven? Seven minus twelve, etc.
The teacher did not find this natural at all. She said she's never seen such behavior. Verifying subtraction with addition was another secret recipe, which school did not disclose yet. Her students were not supposed to understand it.
When I mentioned sticks and stakes in MINUS, MINUS, MINUS-MINUS, I knew I had to write an article about them. Mostly, to explain them better, but also to provide an entry point because they are very useful. This said, please, read the old chapter first.
To numeralize space, we tile the distances with a smaller distance called unit of measurement, and we count the tilings. The actual unit can be only one. We can move it forward, applying its beginning to where its end was.
While doing this, we count in one of two ways. First, we can count the units - the measuring sticks - like I did below.
This is what I call the stick model. It works best, if we can view the whole scene of measurement at once. This means, we must be big enough or soar high above to see the beginnings and the ends of the sticks.
Another way to count emerges where the distances are big, and we are small. The first example of it could have been the milestones of Ancient Rome. Numbering the middles of the miles would not be very practical. The milestones marked the beginnings and the ends of the miles. Standing at a milestone, the travelers knew how far away from Rome they were. I imagine a measuring rope with two stakes. The holes left where the stakes were stuck in the ground are points, and we count them. That's what I call the stake model of distance.
I don't supply the picture for the stake model. It's just a number line. I drew plenty of them for MINUS, MINUS, MINUS-MINUS.
On a small scale, the stake model is awfully problematic because we see too much. Counting the distances from zero, kids must exclude the zero point. For those who are not trained in sticks and stakes, zero is a point like any other. Why don't we count it then? Because zero is nothing? OK, but if we count through zero, we count zero point and exclude some other point, at which we begin.
On a line, we always have one extra point. If we join the endpoints of a line segment to make a contour, they become a single point. Think about a clock face. Oh, no, don't think about a clock face. The English AM/PM system is insane.
The intuition behind the sticks is much more solid. Fortunately, the pieces of paper, on which teachers offer their problems, are always smaller than the students, so the stick model is the best. Like probably every parent, I tell my kids to convert stakes to sticks. If in doubt, draw arcs and count them.
I can imagine an overly smart child drawing arcs between the middles of the sticks and counting them. The rule was explained in MINUS, MINUS, MINUS-MINUS: only distances count. It's a metric space.
In the stick model, there is no zero stick. Zero means no sticks. There was no zero in Ancient Rome too, but they did have so-called Golden Milestone, from which every road was supposed to be measured.
A good method to make stakes palatable involves another heresy: a unary operation of increment. Vitruvius described (but not invented) an odometer, a wheel-based mechanism dropping a pebble preloaded in a hole once a mile. In Ancient Rome, they called pebbles calculi, so the distances could be calculated.
Starting from empty (which was exactly 0), the system would increment the number of the calculi in the receiving compartment. One thought of such a machine running along the number line must be enough to answer every question and obliterate any doubt. Anybody knows where to buy a cheap plastic rendition by any chance? OK then, teach to use increment rather than addition. It's even cheaper.
Drawing one-dimensional sticks and stakes, we have an extra dimension for numbers and letters. In two dimensions, sticks become squares, and we can place our marks inside them. Such squares are handy for measuring areas.
Two-dimensional stakes remain points, and we often use grids to highlight their spatial order. The third dimension is not readily available for drawing. This tempts us to draw points (stakes) as squares (sticks).
A chart of addition on this animated page from STEREOLEARNING is made out of squares. The numbers are inside them. The chart looks like a stick model, but it isn't. Invisible stakes are in the centers of the squares. Zero is in place, and a navigator must skip the first number when counting.
Such transformations are frequent and difficult to understand. Many tables have their actual grids passing through the cells and intersecting inside them.
We must specifically train our kids to understand sticks and stakes. Allow me to give you one more reason why: The chart of multiplication available through this link is a stick model. There is no zero, and we count from the first number.
I don't explicitely teach TLG sticks and stakes yet, but I point out the differences and explain them. From time to time I even offer her problems. Occasionally, I still see her making mistakes trying to use a times table as an addition table.
1 What Color Math?
2 How to Make a Number Line
3 Space Walks
4 Welcome to Debt Hole
5 Poor Physics
6 Through the Looking Glass
7 Do We Live in Burrows?
8 Stick and Stake
9 The minus of a minus
10 Why the Horrors
11 Conclusions
1 What Color Math?
Three years ago, I had to explain subtraction of negative numbers to my child, then 8 years old. As usual, I asked Google what American education was teaching. The page
http://www.purplemath.com/modules/negative2.htm
came out first, as it did today. I looked through it, then through several other Google's favorites, and taught subtraction my way. Use this link to skip this preamble and learn how.
Several days ago, I ran the same query, this time for my youngest American child. I call her TLG or The Little Girl. She was 6 years and 6 months back then.
Now please excuse me, I have to quote this celebrity content before it went away. It is important to understand that the author was a teacher and that she looked for the answer. American math web is huge, and she certainly knew it better than I.
"Whoa! Wait a minute!" you say. "How do you go from ' – (–16)' to ' + 16' in your first step?" This is actually a fairly important concept, and, if you're asking, I'm assuming that your teacher's explanation didn't make much sense to you. So I won't give you a "proper" mathematical explanation of this "the minus of a minus is a plus" rule. Instead, here's a mental picture that I ran across in an algebra newsgroup:
Imagine that you're cooking some kind of stew, but not on a stove. You control the temperature of the stew with magic cubes. These cubes come in two types: hot cubes and cold cubes.
If you add a hot cube (add a positive number), the temperature goes up. If you add a cold cube (add a negative number), the temperature goes down. If you remove a hot cube (subtract a positive number), the temperature goes down. And if you remove a cold cube (subtract a negative number), the temperature goes UP! That is, subtracting a negative is the same as adding a positive.
Now suppose you have some double cubes and some triple cubes. If you add three double-hot cubes (add three-times-positive-two), the temperature goes up by six. And if you remove two triple-cold cubes (subtract two-times-negative-three), you get the same result. That is, –2(–3) = + 6.
There's another analogy that I've been seeing recently. Letting "good" be "positive" and "bad" be "negative", you could say:
good things happening to good people: a good thing good things happening to bad people: a bad thing bad things happening to good people: a bad thing bad things happening to bad people: a good thing
The above isn't a technical explanation or proof, but I hope it makes the "minus of a minus is a plus" and "minus times minus is plus" rules seem a bit more reasonable.
After this page, Google offered a generously illustrated one, comparing negative and positive values to balloons and weights. The third link was to YouTube video, on which somebody was actually adding and taking away red and green cubes, This business was dubbed Conceptual Math, and it was probably inspired by the latest fad in education called manipulatives. In short, no "proper" mathematical or technical explanation (let alone a proof) was in plain view.
The expressions like "the minus of a minus" and "- (-16)" looked interesting. I am gathering such details and dwelling on them because I have never been admitted to American school. I can only try to imagine what do American teachers say and how do they think. By the way, if you are familiar with this project, you know that my goal is not to criticize school or try to improve it in any way. I only want my last child to grow American and stay mathematically enabled.
I believe I know how to subtract a negative number and can explain it in many ways. So I decided to share this knowledge before I die, even though my attempt will probably die even sooner because my math is not purple.
I will start from the most essential information, but please read on to the dessert. If I happen to live long enough, I will work on this article couple more times. I don't have anybody to edit it yet. There can be any number of discrepancies, not to mention my obviously bad English.
2 How to Make a Number Line
If you opened the link, you've seen that the issue was raised after discussing addition and subtraction on a number line. That's where I am going to start.
For the reasons beyond my observations, my bigger American schoolchildren grew to believe that the numbers on a number line belonged to the points, so some of those points were negative. Teaching them back was not easy. With TLG, I started talking about number line before she turned 5. You'll see why. On a properly understood number line the "minus of a minus minus" question simply does not exist.
Suppose you drew a fresh line and marked a point on it. What number is here? You may think it's 0. I may think it's 213. Or 3.07. Nothing in this point has anything to do with any number._______________.________________________Let's now look at the number line. Do we need the numbers on it? If we leave only 0 and 1, will we be able to tell where is 5 or any other point?
0___1___________________________________
We absolutely will. Using the space from 0 to 1, we will walk along the line counting. The count of the steps from 0 to another point will tell the number at this point.
To make a line a number line, we need two points. They can be anywhere, but once we made a choice, we are bound to stick with it, or it will be another number line. The points are designated as 0 and 1.
A point has no width, length or height. There is nothing to count or measure in it. No point is bigger or smaller than another point. Several points do make a quantity, but they don't make a line. We could as well line up some counting tokens.
The quantity is enclosed between any two points. It can be compared to the likes of it, and what can be compared can be measured. It's called distance. Look, di-stance. To build a number line, we don't even need the 1 point. We need the distance and the direction to it.
Only two points matter. A distance is a property of a line segment, and any segment is between its beginning and its end. A point labeled 5 has no quantity. The label indicates the number of the steps from 0 to this point.
Distance is always positive because our space is isotropic, which means, it's the same in any direction. Coincidentally, I just finished a new project, in which I tried to explain and demonstrate how important it is to teach isotropic thinking.
The negative numbers to the left from zero are not distances. This little secret of the number line causes all the problems. To find the point for a negative number, we count from 0 to the left. The counts and the distances, however, can only be positive.
The model of space with two infinities and zero between them seems so natural that we may not even notice how passing through zero we change the direction of counting. Everywhere on the number line we may count the distances in any direction. To find them from the numbers, we have to subtract the left one (which is supposed to be smaller) from the right one. Labeling the points on the right we add the distances to 0, while on the left we subtract them from 0.
Let me read this one more time. Did I get it right? Are you sure?
Space comes without arrows and numbers. The arrows and numbers were introduced to numeralize space. It's not clear who and when decided to use a number line to teach math, but it must have happened much later than the first numbered Roman milestone was erected.
At some point, some Ancient Roman must have realized that the milestones are not only telling the distance to and from Rome. On the same road, they allow to figure out the distance between any two of them without counting the calculi again, simply by subtracting the smaller number from the bigger one.
The "as the crow flies" distance between Boston and New York is 190 miles. From New York to Boston it's 190 miles too. Without wind and other encumbrances, the fly time and the energy expenditure will be the same. Subtracting a bigger number from a smaller number today, we get a negative number, which must be smaller than a positive number, but represents the same flight or the stretch of the road!
How to subtract a negative number anyway?
Consider the distance to Rome. To find the distance between 0 and 5, we subtract 0 from 5. OK then, what's the distance between -5 and 0? Of course it's 5, but how to find it from the numbers? I mean, how else can we do it?
3 Space Walks
To obliterate any doubt, we can move 0 and 1. After all, 0 is just our observation point, and 1 is the end of our measuring stick. Moving 0 and 1 while keeping the distance between them the same, changes every number by the distance of the move. The distances between all other points remain unchanged.
| |
-2__-1___0__+1__+2__+3__+4__+5__+6__+7__+8__+9__
| |
-4__-3__-2__-1___0__+1__+2__+3__+4__+5__+6__+7__
| |
-6__-5__-4__-3__-2__-1___0__+1__+2__+3__+4__+5__
| |
-9__-8__-7__-6__-5__-4__-3__-2__-1___0__+1__+2__
+6 - +2 = +4 - 0 = +2 - -2 = -1 - -5 = 4
I set up two pins. They were at +2 and +6. I moved 0 and 1 two 1s to the right, and the pins appeared to be at 0 and +4. Then at -2 and +2. Finally, at -5 and -1. The distance between the pins has always been 4, and nothing else. A child of any teachable age understands this.
The static example with +5, 0 and -5 can be easier to remember, but a sliding number line allows to enter the weirdness, go through it and exit from the other side. I offered both to TLG and she understood them quite easily.
The moving 0 and 1 could have been studied with a ruler, or, better yet, a measuring tape with 0 in the middle. Swapping 0 and 1 and changing the distances between them is even funnier. The tricks like these are essential for understanding number line.
Early arithmetic is about counting and whole numbers. A number line looks like a collection of the numbered points. The kids ignore the line, they count the points to find the numbers. Without the line and the distances though, we would not even find the points to count. It's just a bijection? OK, but why this one?
4 Welcome to Debt Hole
The original meaning of "negative" quantity most likely was: it's a void, but we know how big it is. Debt comes to mind first, and debt is essential for early education. The notion that getting rid of something you owe makes you richer is very obvious.
And it's a rich subject, conceptually. Mom gave you $20 to pay to school cafeteria. It turned out, US Government just realized that if it thinks it has to teach every child, it has to feed them first, and now your family do not owe anything. Somebody surely became $20 richer, but was it you or your mom?
In practical calculations, we avoid negative quantities and numbers by separating negative and positive spaces. We say we have debt. A shopping list is the negative inventory, but do we care? We just use different names for them. If we need to bridge the negative and the positive areas, we count from a negative number to zero using positive 1s.
In this post, I demonstrated how it is possible to represent negative values as holes and build shnumbers out of them. A hole is a good metaphor for debt because holes are inversions of things. An abstract thing can be it's hole turned inside out.
Adapting the hole model for a whole-number line is easy. It can also cover real numbers (see X-bag).
Suppose there is a stack extending from minus infinity to some point on the right from zero. It's neither negative, nor positive. It's just a stack, and it's the same everywhere. For some reasons, we consume this stack. Maybe it's edible (and tasty) or valuable. Can it be a stack of coins? Or cookies?
Turning the following pictures 90° counterclockwise would not be better. I tried.
Every once in a while, we subtract a piece of the stack - a cookie or two - and spent it. At some moment, we came to zero and learned that the left part of the cookie stack belongs to somebody else. To infinitely many owners, probably, because it's infinitely long. Can it belong to school cafeteria? Good thing, the owners agreed to lend us some of their cookies. By the way, we can turn the table and imagine it's us are lending cookies to someone else.
This way or another, somebody keeps chewing on the stack digging the hole in the wall, so the hole - the distance between the wall and the end of the stack - is growing. Every time a piece of the stack is subtracted, the same quantity adds to the hole.
To the left from 0, we can't count the cookies anymore. At any moment there is an infinite quantity of them left. The debt hole brings about a new king of quantity because we can measure the depth of it. If we decide to pay it off, we will be adding to the stack and subtracting from the hole. To return from NCW (net cookie worth) of -23 to +19, one got to pave the way with real cookies, as positive as they get.
Why cookie line is so understandable, and number line was not? Consider the distance from NCW 5 to NCW 10, It's equal to 5, right? However, when we go from 10 to 5 we take 5 cookies, and to go from 5 to 10 we have to bring 5 cookies. Dealing with things in space we see or imagine what we do.
Another reason cookie line if friendly: the negative space is meaningfully different from the positive space. Coloring number lines is nothing compared to debt hole.
5 Poor Physics
Of purpular math wisdoms, I would single out the idea that negative is bad and positive is good. Just think of electricity. Technically, however, the hot and cold cubes are worse, not to mention balloons and weights. That was, of course, my incompetent opinion.
The cold and hot cubes seem to be wrong in so many aspects, I don't even know where to start. Besides, this mathematical physics is too hilarious. OK, thermometer scale is not a number line - there is absolute zero - and positive degrees are no different from negative degrees. A hot cube can only affect the temperature of the "stew" becoming cold. Once it's heat passed to the stew, there is no way to take it back, unless we employ one of those creatures called Maxwell's demons. If cubes were heaters, they would need energy (wires?), and if they were coolers... OK, OK. The idea is perfectly fine. Didn't the teacher mention that the cubes are magic? If magic is that they teach, this explains everything.
Without magic, school math to me is the best taught subject. Instead of using physics, let alone teaching it, schools screw it up in every possible way. But - please excuse me - what positive knowledge can be built on fundamentally wrong analogies?
For centuries, physicists and engineers had been converting every quantity to the scales of line segments so we could see them. The 0 on thermometer scale simply appears closer to our operating range. The situation with time is similar, but harder to understand. Time could have begun too long time ago, and we don't know exactly when. Besides, our BC/AD system is lacking 0.
If we can avoid negative numbers counting money and things, and even thermometer scales belongs to the positive half of a number line, where in the world number lines and coordinate systems based on them are being used?
In math, of course. Math is a part of this world, and the biggest one. Otherwise, Euclidean space (generalized as a metric space, or space with distances) is a model of physical space, period. The answer to "the minus of a minus" must be found between the two. If it was not understood, we got to teach better.
Magical cooking and gravity are distracting at best. Another analogy - the one with balloons and weights - no matter how oversimplified, is about two forces, and forces are spatial.
The mathematical model fits only if physical space is isotropic (or, at least, isotropic enough). In isotropic space, there is no zero point. The distance to the first point and direction to it is not marked. Where did all this stuff come from?
From our imagination. Coordinate system is our body in space. Call it an avatar if you like. The point marked 0 is our point of view. It can be anywhere because we assume that space has no beginning. The point marked 1 is the end of the body part, which we use for measuring (like, for example, cubit or foot). The rest of our spatial intuition is derived from experimenting with solid objects, but it only makes sense if we imagine ourselves among them.
Unfortunately, our spatial experience is crippled with gravity and limited by Earth. Another complication is our body plan. We are most capable in one direction, which we identify as right and left. That's barely enough to operate on a two-dimensional plane. The common Cartesian 3D coordinate system is for the monsters with three arms.
A number line, which is a 1D coordinate system, is not so demanding. To play with distances, I use a compass or tile a number line with material objects. Cubes (unless one wants to promote them) are just not right for this. I have matchsticks.
6 Through the Looking Glass
A number line would look like it has a mirror in the middle, if not for those annoying minuses. Let's use colors instead, or stick less obnoxious labels like left and right.
Mirroring provides another look at the "minus of a minus" problem. Here is what we have:
1 = -1 -1 = 1
Everything looks perfectly normal, is it?
But then
1 = --1 --1 = 1
Indeed, if one minus makes blue red and red blue, two minuses circle the colors around.
What makes students miserable is just a notation, a sign of subtraction before a number. When I learned about negative numbers, I thought that the minus signs in front of them meant unsatisfied subtractions. The hungry monsters were ready to take a bite from a positive number or swallow it completely. It did not take long to understand that positive numbers were treating negative numbers just as nicely.
This left a strong sense of misgiving. If we bring together 1 and 1, they will be 11. While -1 and 1 turn into -11, 1 and -1 become 0. Finally, -1 and -1 make -2. Something is profoundly wrong here, don't you think? I do.
7 Do We Live in Burrows?
I'm afraid, the content of this chapter must be X-rated. Nothing from it may be used or mentioned at school. It will not end up well.
Using the red-blue notation, how could we perform the operations? Is a blue number just a negative number without the minus sign?
It can be. Or it can be positive. Or both red and blue can be positive. Or negative. Only the rules of operations would be reworded. Like, for example, in case of all-positive we would add blue and red to find the distance, but we can keep calling this addition subtraction like teachers told us to do.
Seriously, we have three points in a line: A, B, C (in that order). We know the distances from A to B and from B to C. What's the distance from A to C? How school messes up our sense or reality to make this problem not obvious?
Remember the stack of cookies? In this model, the negative and the positive values were different. Debt was a hole, no matter what color I might paint it.
In space, the reality on the left from zero is no different from what we see on the right. Moving, mirroring, rotating the coordinates do nothing. We certainly can not turn open space into a burrow or change it in any way.
Familiar number line is very weird. The minus signs on it do not just tell that their bearers are located to the left from zero. The negative values must be smaller than their positive counterparts. Please excuse me, a space like this is my home. It's not what I see.
Remember, the distances related to the negative numbers are all positive. Why negative numbers are smaller then?
Because teachers told us so. Yet it only makes sense while we are counting (measuring) things. Things can be arranged in space. They are not space. Space itself is different. It has no zero, to begin with. We can move zero along, making the negative places positive and the positive places negative.
Dealing with coins and cookies, sticks and ropes, paper and plywood, water and sand, we know what is zero. Zero means we have no coins or rope. As long as we exist, we can't have no space.
Suppose an Ancient Rome road was there before Rome was build. Then, the builders put the golden milestone in the middle of it. Could it make one half of it negative? Or can it just have two positive halves?
On the ancient road, we could use North and South miles. Adding North to North and South to South, we would move away from the golden milestone. Subtracting North from North or South from South would brings us closer to the golden milestone first, then to the other side from it. Adding North to South or South to North would be like subtracting the same direction miles. Subtracting South from North or North from South would be like adding the same direction miles.
A bigger number would mean the bigger distance from the golden mile, either way. The North and South numbers could be negative or positive. A negative North would be South and the negative South would be North. Now, would the distance between a South milestone and a North milestone be South or North? Or something else?
In space, there would be no reason to prefer North or South. Not so with numbers. It is usually assumed that the natural numbers are positive. Even if they are not, the positive whole and real numbers are bigger than the negative numbers.
Negative numbers make sense for counting/measuring things. Applying them to space was an insanity, which schools forced us to accept. Well, the unified model works. It covers not only space, but credit too. It just challenges our intuition, particularly so because the number line itself is a one-dimensional space.
But then, how many people look at those minuses every day? How many of them cry foul before the teacher asked to subtract? And are you still sure that the students who have troubles understanding number line are the dumbest?
8 Stick and Stake
Since a number line is a matter of distances, can we number them? We can, but some teachers may find the following instructions disturbing. Don't try to do it at school.
I took a liberty to introduce a new unit of measurement: one shoe. And it's not just a name. I will actually use two shoes as the measuring sticks.
Here are three right shoes on the shoe line (or call it +3 if you like).
Then, here is 3 - 5
Shoes are vectors in disguise, and they are countable. I can use shoes to introduce displacement. And again, I don't see the "minus of a minus" trouble with them.
That's how I make a negative shoe positive and a positive shoe negative. It's so obvious that I could safely label the left shoe with "-" and the right shoe with "+".
Sure enough
Walking through the looking glass is not different from counting away, but it may seem weird. The 1st and the 2nd shoes have the 1st shoe between their heels and the 2nd shoe between their toes. Either way, it's 1 shoe. Both the left 1st and the right 1st shoes are between their toes and they have 0 shoes between their heels. Well, we wanted two infinities.
Speaking of 0, there is no shoe for it. A shoe is a shoe, and 0 is nothing. Zero is simply no shoes.
Not only shoes can be negative and positive - they can walk negatively and positively. This will be useful for multiplication.
We can walk through 0 in four different ways and represent our paths accordingly. It can be counted in the positive (forward walking) shoes, left or right, or in the negative, backward walking. The count will be positive and distance will be the same. We just measure it differently. To me this proves that, unlike the numbers, the shoes cover the space adequately.
In one-dimensional space of a number line, a right shoe can be a plus one, and a left show a minus one, so we can start incrementing and decrementing. We can also play with real numbers. Important difference is that a right shoe is no smaller (let alone better) than a left shoe.
Remember the lack of 0 in BC/AD? I believe, this "the measuring stick" or just the stick model of spatial quantity emerges early in life even if we don't teach it. It works while we operate with small distances using our body parts and seeing the whole scene at once. Transition to the "measuring rope with two stakes" or just the stake model is clear. As we begin measuring and think big, we become small. Our body is a point compared to a mile. That's when we get milestones, number lines, an extra point for every stretch of space and zero as a number. A point can stand for 0 because a point is nothing too.
Two models coexist, and the differences between them causes troubles in learning. The stick is better for the scale of the school number lines. A countless number of times, I had to tell to kids: Never mind the points, count your steps, draw the arches.
An extra point or stake, which messes up counting and disappears if we join the ends of a segment to make a contour, is particularly troubling. I can easily think of toys to address and eliminate this issue long before school - once I searched for them and could not find anything - but this would be too much of a digression.
I believe we have to teach the stick model explicitly and compare it to the stake model at every opportunity. To me, the stick model is just a shnumber line, doubled up and enhanced with vectors. Vector is another "advanced" concept, which very young kids can learn and use in two dimensions.
9 The Minus of a Minus
Trying to read the teacher's mind (because I have no choice), I can only assume that she understood the red minus in
a-(-b))
as a function. It could have been framed as a function, but it was not. To my uneducated eye, we are dealing with three different roles of this humble glyph.
The outer (red) minus must be a sign of operation of subtraction, which in our numeral system is distinctly different from addition, and no algebra can change this fact. I mean, subtraction can be be merely an addition of a negative number, but dealing with numbers we have to subtract.
To my taste, the common method of subtraction is too different from addition. In STEREO LEARNING I described a fully reversible addition, but it needs to be reversed and applied anyway. In the end of this article I will demonstrate a numeral system, in which subtraction can be diced altogether, but this system is for another planet.
Subtraction is a binary operation. It takes two operands, and the minus sign stands between them.
Next meaning: a minus can indicate a negative number. If it stands before the number, this number must be subtracted from 0.
It looks like nothing else can be found in the Books of Education. A sole minus what does not indicate a negative value like in -(-5) appears to throws students and teachers alike into cognitive dissonance.
The painless way to understand a single minus before a number or a variable, is to consider it to be a sign of a unary operation, which makes a "negative" value "positive" and a "positive" value "negative". I prefer to call it inversion. From the point of view of arithmetic, inversion can be understood as a subtraction from 0 or as a multiplication by a negative 1.
I told more about inversion in this post. Let me also mention that unary operations do not require parentheses, affectionately known as "banana peels". You may just go through the signs in -----------7 and discard every pair of them because they cancel each other.
If the number of the minus signs was odd, the last of them would survive, and we have to subtract. If the number of the minuses was even, we have to add, but there is no + signs in expressions like
a - -b
I can be wrong, but, as far as I remember, the bulletproof method of pre-reform math was to replace every two consecutive minuses with a plus, non regarding to the arity of them. Banana peels must prevent students from doing this.
10 Why the Horrors?
We can explain, and a reasonably smart modern children can understand this explanation by their 7 or 8 years, provided that we teach them instead of dumbing into millennia-old wizardry.
Recently, I taught TLG, who was 6 years and 3 months old, the method of subtraction described in this chapter. It's not even a method, it's a standard algorithm applied without fear, favor or prejudice. It allows to inverse a "positive" number subtracting it from 0, and then inverse the resulted "negative" number the same way to get the original number back.
TLG liked this trick so much that it took me several lessons to return her to the government-sponsored subtraction. As usual, I said that teachers are not going to allow this, but there were other reasons. For example, it's not easy to spot even that …981 = -19.
The big reason behind numerological nightmares is that the numbers below zero are not represented in the ancient Hindu-Arabic numeral system, which we still use.
The concept is a piece of cake. The problem is how to deliver it. Keeping minus in front of every negative numeral wouldn't be very unhelpful. Alternative methods include using different colors, underlining/overlining the numerals or turning them upside down. I decided to use three colors. This solution looks ugly, but it works.
I am going to use a handy quinary notation with the numerals 2, 1, 0, 1, 2. One negative numeral would be enough. I just wanted to ensure equal (balanced) representation.
I provide the chart of addition (the left one below) in diagonal form, as introduced in SHNUMBERS. The regular positive-only chart is on the right. The stricken-through cells are the coordinates. The numbers on them are the addends. The sum is found as usual. Going through the counting below you will understand how the system works.
Let's count forwward from 0. In parentheses, I explain every number using our trusted Hindu-Arabic system.
1 (1)
2 (2)
12 (5 - 2 = 3)
11 (5 - 1 = 4)
10 (5)
Allow me to remind you that in this quinary or base-5 system the weight of the positions are 1, 5, 25, 125 and so on. Hence, 10 is equal to Hindu-Arabic 5. The numbers between Hindu-Arabic 2 and 5 are made with blue numerals: 11 means 5 - 1 and makes Hindu-Arabic 4.
I didn't have much trouble counting because I imagined a number wheel counter, in which the wheels were changed to accommodate 5 numerals and relabeled.
Let's count forward a bit more.
11 (5 + 1 = 6) 12 (5 + 2 = 7) 22 (10 - 2 = 8) 21 (10 - 1 = 9) 20 (10) 21 (10 + 1 = 11) 22 (10 + 2 = 12) 122 (25 - 10 - 2 = 13)
The numbers look longer because they are quinary. Subtraction is possible but optional. Subtracting, you don't have to put a bigger number first and change the sign. To invert a number, invert every numeral in it. For example, 122 (that's 13) becomes 122 (-25 + 10 + 2 = -13). Then you can just add it.
I hope it was enough to understand that balanced notations stop discrimination of the blue or left-hand numbers (until, of course, we learn multiplication). Likening subtraction of a negative number to multiplication of two negative numbers (in the language of Purple Math, "minus of a minus is a plus" and "minus times minus is plus") was just another instance of educational magic.
"The minus of a minus" problem is very closely related to division by a fractional number (so-called "invert and multiply" rule), but I've never heard of teachers associating them.
I am sure I could teach TLG the balanced notation, but I am not going to do it yet. We have different priorities. I want long multiplication (with distributivity, exponentiation and other bells and whistles) to settle down first. Looks like TLG will be there before she'll turn 7. Then we will have plenty of time for this and many other mathematical treats.
The balanced notation can replace the positive-only one. It leaves up to us how to use it. We can still assume that the red numbers are bigger or count the shoes.
11 Conclusions
Negative quantities and numbers are being mistaught, and, upon closer examination, I found that it's much worse that I thought. Number lines, widely used as a helping device, are particularly bad. They complicate understanding of operations and they are downright confusing for marking up space.
As you could see in the debt hole chapter, in the model using things in space, in which a negative number is an empty space (hole) extending all the way to positive infinity, and a positive number is a filled space starting in negative infinity, the operations are very natural and easy to understand.
This model is not at all exotic. We still see it in liquid-filled thermometers, in bar indicators (usually simulated on computer displays) and in bar diagrams. The modern designers often spoil it, drawing the negative values as the bars extending down or to the left from 0.
The nature of the hole is different, but it's an interval. I taught TLG that the negative numbers are holes without using the metaphor of a debt hole represented as a burrow. It was just a filled and unfilled space, always counted or measured from zero, which is the only possible way to do it. Adding a positive number to a negative number, we fill the emptiness first. Adding a negative number to a positive number, we clean some space.
TLG quickly learned to use regular number lines. Every time I saw her confused (and I am good at it), I could say: "Remember, a negative number is a hole". In her experience, it wasn't a debt hole though. Handling shnumbers on a pegboard, she did have the holes.
Using number lines in coordinate systems, we parents have to understand, remember and teach that a number line is a special case and a common implementation of a general model with two infinities and zero between them. The negative numbers have nothing to do with space. We have and use some other notations like, for example, the relative or cardinal directions, if not explicitly vectors.
A proven way to make them very mad.
The shnumber on the board is equal to -30814. How? I made it out of holes, or empty spaces, and turned upside down.
Telling such shnumber is relatively easy. Making operations with holes requires silencing your intuition and following the rules. This is quintessential for mathematics. Just try.
Besides being a brain twister, such shnumbers are models of negative quantities. Male elements are ones, female elements are minus ones (please excuse me for being an electronics engineer). When the hole is filled, it becomes zero.
This model once made TLG's little sister very frustrated. I did not offer it to TLG yet.
Putting a positive board on top of a negative board, we can add up negative and positive quantities. Fortunately, there are other ways to do it, because filling boards with pegs is taxing. Unfortunately, I can't offer or recommend a computer program for such manipulations. You can drag and snap circles using any free object-oriented editor, don't even think of letting kids do it though, because of the presence of the shape-changing controls.
Remark that adding a positive number to a negative number you perform subtraction (with "borrowing"), but nothing prevents you from subtracting bigger number from smaller number. You simply end up with unfilled holes.
Making connections between representations
In SHNUMBERS, I disclosed that I am an oversimplificator. I am simply not smart enough to understand and appreciate the subjects like reform math. To me this reform means that teachers got science off their backs, and happily allowed themselves not to teach. The school is now free, and nothing in this democracy can bring it under control.
I wish it was so simple. In reality, school keeps itself employed imitating teaching. It looks like they throw at the students everything in hope something may stick (guess, that's how they understand the multiple embodiment principle). Knowing arithmetic is no longer enough, and, actually, is not even required. The students got to learn the silly stuff, call it common core or whatever. Or else.
"Standards" (another name for silly stuff meant to keep teachers busy) can be good for bad students. They may not know how to multiply, but if they learned to look up the data in the linear tables or recognize the patterns like 13579, this would be something.
School operates under an assumption that a standard American student can not learn multiplication. I don't believe in this, but I have something else to care. What if my children can? School make them learn as if they could not, or punish. Trust an immigrant, who can't even speak decent English: teachers still think that they are surrounded with cavemen, and believe they are the ones who carry the torch.
Even for the teachers, picking and getting the silly stuff falling from above is hard. The best defense I can think of as a parent is: aim high. Teach representations that may knock the reformers' socks off.
Here is a recent example. I have a plastic jar with 1000 1 cm cubes, like the ones in Dienes sets. We don't open it often. The cubes are too small, poorly made, and the colors are ugly.
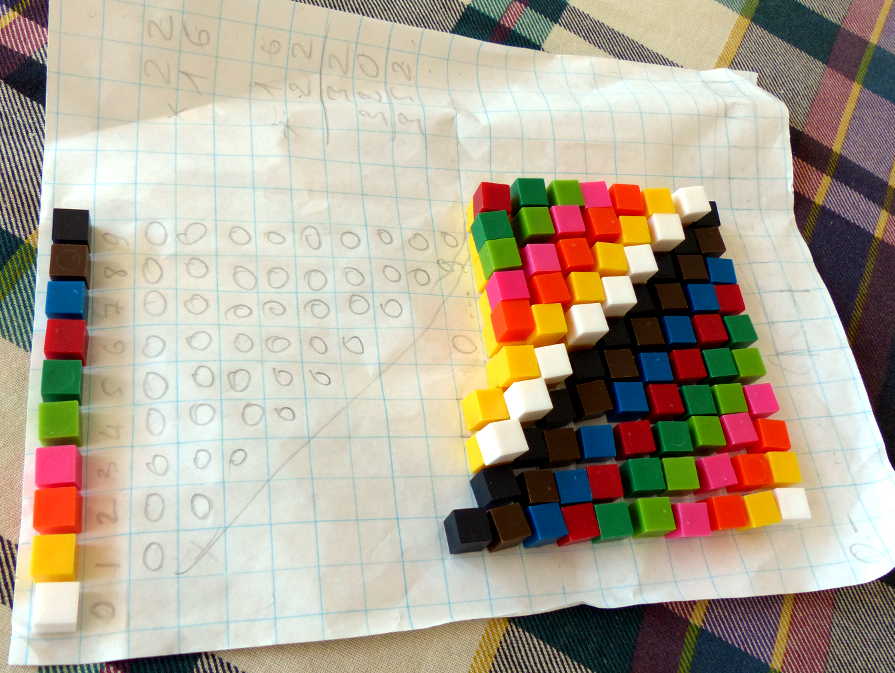
Suddenly, I realized that there were 10 colors in the set. I built the table linking them to numerals and suggested to perform computations in colors. This did not make TLG happy - she hates everything new - but she quickly got the idea. By the following lesson, she remembered them all (I did not) and called the colors by their numeral names quite confidently.
I challenged TLG to build the chart of additions in color. She agreed, but I had to do the gluing. Otherwise, she wold probably get mad at me because the idea became too simple to her to be exciting.
So TLG was telling me which color to glue next, and we ended up with what you see on the picture. We could not finish it because I ran out of glue dots, but the progress was convincing enough.
Teaching at home, I present new concepts from different angles or try to derive them from what TLG has learned before (not necessarily in mathematics), but it's not multiple embodiments. Even at it's finest, the idea of multiple embodiment contradict all my learning and teaching experience. I believe the abstract ideas must be acquired on some familiar substrate. I use pegboards a lot, TLG's intellectual life has been revolving around those awful pegboards since she was 2 years and 4 months old.
This said, there is a similar problem, which American school with it's dependence on formal testing greatly amplifies. Once kids learn notation, they quickly forget what it means. They may know how to use it, but in the core their knowledge is absurd. I am constantly trying to break the ice, offering new disguises for well studied concepts. In the language of reform math, I want them to make connections between concepts and representation.
Tracking the invisible quantity.
Please allow me one more quote from Wikipedia. It's not supposed to be an authoritative source, but you know what Wikipedia really is.
The American Institutes for Research (AIR) reported in 2005 that the NCTM proposals "risk exposing students to unrealistically advanced mathematics content in the early grades."[14] This is in reference to NCTM's recommendation that algebraic concepts, such as understanding patterns and properties like commutativity (2+3=3+2), should be taught as early as first grade.
This is sad, but again, I am not in charge of "most students". TLG knows and uses commutativity since she learned addition, and she learned long addition before she turned five. Putting a bigger number first, always makes computation easier. Associativity? Adding something like 1+7+9, she applies 1 to 9. There is no positional arithmetic without algebra. And let me remind you what a regular minority kid could do with patterns.
TLG can use formulas. Absolutely. The notion that young kids can't learn such things is either ignorance or deliberate manipulation. Big kids, who underwent many years of brain stiffening treatment at school, do have troubles learning to use names and roles for numbers. Small kids, who learn naming things, don't.
When TLG's faint-hearted big sister was learning positional addition on shnumbers, I explained to her elementary algebra using letters for colors. R is the red quantity, B is the blue. It was perfectly fine. Several months later, my suggestion to use letters for numbers made her upset. I reminded her she did it with pegs. She recalled this, but now she knew that letters were pre-algebra, and pre-algebra was to be afraid of. I believe, that's how I've heard about pre-algebra for the first time.
In the beginning of the forth grade, she mentioned that the next year she would start pre-algebra and said she was scared of it. I assured her that she already knew this silly subject, and taught her recurrence relations.
While I was teaching TLG's big sister, the other kids, or, maybe, even the teachers (the art teacher, quite probably), were telling her the horror stories. That's how school controls the population.
Soon after TLG turned four, I took a plain paper bag and crossed it corner to corner with red marker. This device came to be known as the X-bag. Another one was the Y-bag. At first, I was stuffing the bags with counting bears, and TLG was keeping tracks of my additions. Then I started asking questions like: if I put 3 more bears in the bag, there will be 8 of them. What the mystery number X is equal to?
TLG quickly understood equations and started solving them. Guess, for the time being her method is good enough because she is still learning how addition and subtraction work together. By the way, she learned about negative numbers and zero from her mom before she turned 4, and her understanding is very solid. I tried to catch her many times.
Recently, I returned the X and Y bags on stage. TLG remembered them, and was happy to see them again. We moved some pegs back and forth carefully watching and tracking additions and subtractions as they occurred. Next we moved paper cards with big numbers.
She is just a little girl.
I introduced TLG (The Little Girl) in MAKE THEM MAD, and even "shared" two pictures of her taken when she was much younger. She does not look nearly like this. She is six years old, and she just started her kindergarten year.
I am still homeschooling TLG. My goal is to teach her numeracy, not leaving reform math any chance. She just started doing long subtraction (10 digits and more), she knows all the operations (and she even understands they are operations) and she got many gifts from pre-algebra treasure chest. Or, maybe, algebra. I don't care what they teach any more.According to its proponents, reform math was supposed to be a blessing for women and minorities. TLG is a girl. She is an offsprings of a pretty poor minority (and a very small minority, as a matter of fact). Yet it does not look like she belongs to "most students" of Steven Leinwand's article.
On average, our lesson takes 30 minutes per day, and it's not only numbers. I would much prefer to do something else, but we can't afford much of it. TLG just told me, pointing at her forehead, that she constantly reminds herself not to hate math after the first grade. I only mentioned it, maybe, couple times, when she did not want to learn.
Otherwise TLG is a normal American girl, and her interests are normal for this part of the population too, except she is more advanced than her peers in every aspect. It's not my words, it's official. Fortunately, the officials have no idea how advanced, and, most importantly, how different she is. They prefer to be professionally blindsided. As for TLG, I am telling her that truly smart people do not show how smart they are.
Which I prefer to call reciprocation.
Multiplication is repeated addition. Division is repeated subtraction. We can always multiply two integer numbers. Occasionally, we can also divide one number by another one and get yet another integer number.
To make division always possible, we need rational numbers. Rational numbers are combinations of integer number and fractions. Once we admitted them to the scene, we understood that every integer number can produce a pair of rational numbers: We only need to divide it by one and divide one by it. Where we had 9, we now have 9/1 and 1/9.
Remember the meaning of the words numerator and denominator: 9/1 means nine of ones. Like any number, 9 is just a bunch of 1s.
This brings about another unary operation of inversion, which I like to call reciprocation. It turns 1/N to N/1 and back.
Forget fractions, what do you do to divide by a whole number? You reciprocate it, so that 9/1 becomes 1/9, and multiply. Dealing with any other rational number, you just do the same.
The first inversion - the one turning negative to positive and positive to negative - could be understood as subtraction from 0 or multiplication by -1. Reciprocation of a number can be understood as division of 1 by this number or as power -1 of this number.
School shows mathematical machine wiggling its limbs. Make the cover transparent. Let kids see how it works.
Kids know them, teachers don't.
From different students of different elementary schools, I heard that many in their classes knew about negative numbers, yet the teachers were telling them that it is not possible to subtract a bigger number from a smaller one.
If your student is smart enough to understand negative numbers, why would not you try to perform a forbidden subtraction? What, for example, is 203-447? I am not sure how exactly they do subtraction in reformed US schools, so I tried to make it very clear.
The first line on the illustration has position numbers. The blackened and underlined position is where we are. Click on FORTH and watch. When you reached #3, please remember that spaces in front of a positional number (as well as behind it) is, in fact, the infinite line of zeros. Without them even addition would not be possible.
Remark that FORTH is on the left from BACK. That's because we Europeans have borrowed positional numeral system from Arabs together with their writing order.After #5 the demonstration ends. Clearly, we can go like this forever. I put … in front 9 to indicate that the infinite line of 0s became the infinite line of 9s. Few extra 9s were for clarity. …9 or …0 would (and will) be enough.
The infinite line of 9s looks scary, but no scarier than a periodic fraction. I decide not to use any special mark (like vinculum on top of a periodic part). For this demo an ellipsis before 9 is good enough.
We could do subtraction in strict accordance with the rules, and we can do it for any other two numbers, putting the smaller one first, but what's the use of those forever nine numerical freaks?
Let's try to add 447 to …9756. Here is how.
Going like this forever, we will get …0203, or just 203. Remark that it was not subtraction. Just plain addition. Is …9756 secretly equal to -244?
It's no different. Try do add it to some other numbers, big and small, to make sure that we found a perfectly workable representation of negative quantity, which eliminates subtraction entirely.
Wait a moment, how about number sense? An infinite line of 9s looks like an awful lot!
No matter how it looks, the biggest whole positional number …9 (an infinitely big whole number made entirely of nines) is just one smaller that 0. Try to add 1 to …9. It becomes 0. This can only mean that …9=-1 (…9.9…, which is infinite 9 to the left and infinite 9 to the right from the decimal point, is infinitely approaching 0).
This means, in turn, that our familiar number line is actually an infinitely wide circle. The biggest number we can think of approaches 0 from the other side.
Remark though, that this observation is not about quantity or geometry. It's about positional numeral system. It would not make much sense, for example, to ask infinitely deep questions like will the wave of additions will ever catch up with the wave of subtractions. Once they traveled out of view and far enough, we can use the visible part like there is nothing to the left from it. After all, there are no infinite positional numbers in real life.
Just couple more paragraphs, OK? …90=-10, …900=-100 and so forth. The number …9756 is -1000+756=-244, precisely as expected. Or how about multiplication?
…9756+…9756+…9756=…9268
Please don't think that this chapter was a singular pointless bump on the smooth road to numeracy. If you got it, you will easily understand how machines, including computers, handle quantities. And I have more to tell.
I've never happened to teach negative numbers. Every student in my life, big or little, already knew them. The knowledge of infinity is not so common, but every kid was pretty comfortable learning it.
Not a sign, but an operation to change it.
Mathematics is so notoriously difficult to learn because education is so conservative and selfish. They teach like many hundreds years progress never happened. They squirrel away every helpful invention and discovery and turn it into an obstacle to learning. Mathematics, which is tremendously useful and empowering, they present as a scare.Without introducing anything new, let's just rewire the teaching. I will use a simple and exciting narrative: people were inventing new operations, they tried to reverse them, and every time this led to a discovery of a new kind of number.
The most basic operations are counting (increment) and counting back (decrement). Teaching them as such (like some preschool educators do) to me is simply impractical. Before you explain them to kids, they know numbers, so increment inevitably turns into +1. Still increment and decrement are very handy for teaching, and they allow us to introduce unary operations.
Incrementing many times at once is what we call addition. In positional system it's not just another name. We have a method, which makes addition much easier. Not even much easier, but exponentially easier. Demonstration of how positional addition is easier than counting forward is breathtaking (since I wrote this, I spent another month and produced STEREO LEARNING to illustrate some of such statements).
Repeated decrementing leads to subtraction, and we face the problem of numbers for the first time. We can always add two numbers. Incredibly, there alway is a natural number waiting to be discovered through addition. Yet we can not always perform subtraction. We need negative numbers to make it possible.
This kind of reasoning becomes available after we exposed our children to big numbers, which school does not do. Well, without big numbers you can only leave the learners to discover their knowledge and conceptual thinking. I keep picking on conceptual thinking because it's such a shameless lie. On par with calling a daycare an Academy.
As soon as we invented negative numbers, we understand that natural numbers - the only kind of numbers we knew before - are positive. Or we may think that every natural number can produce a pair of integer numbers if you add it to 0 and subtract from it.
Next comes another unary operation, which can be rightfully called inversion. I often call it negation, which is worse because of asymmetry. At school they do not teach such things. I wonder if Steven Leinwand knew that inversion is an operation.
Inversion turns negative numbers to positive and back. One way to do it is subtracting from 0. Another, and more interesting way, is multiplying by -1. In fact, -1 is the only negative number we need to build the rest of them.
The true meaning of the minus sign is the operation of inversion. Now what do you do to subtract a negative number? Yes. You invert and add.
Is it so easy? Of course it's not. Soon I will return to subtraction to discuss the problems with it. Elementary math is actually a toxic swamp. Allowing children to "discover" it without guidance is inhuman.
Theirs but to do and die
First thing first: the line came from this poem. At the Battle of Balaclava (no, not that balaclava, Balaclava is a town near Sevastopol in Crimea (yes, this Crimea)), which happened during Crimean War, a 600-strong British light cavalry detachment was sent to attack a powerful and well guarded Russian battery through so-called valley of Death. Apparently, due to their commander's mistake.
Next...
Theirs not to make reply,
Theirs not to reason why,
Theirs but to do and die:
Not all of them died, and those who did not, inspired another famous poem, but you better read the article.
What British cavalry was doing in Crimea is another story, and a very interesting one. Wikipedia has it too.
It took me years to realize that the "do and die" attitude was one of the biggest difficulties my wimpy kids were facing at schools. They were raised to understand. American school demanded blind obedience. I failed to prepare them for this.
Before answering why (invert and multiply), let me tell you that this must be the second inversion to learn. The first is invert and add.
Just invert and multiply
The name of Steven Leinwand's article was "It's Time To Abandon Computational Algorithms". He explained what exactly had to be abandoned in the following words.
...the formal, paper-and-pencil computational algorithms that constitute the core grade-school mathematical experiences of most American youngsters. It's about mindless procedures like "carrying threes into the tens column,'' "six times seven is 42, put down two and carry the four,'' and "eight from two, can't do, cross out the five, make it a four, and borrow 10.'' It's also about memorized rules like "yours is not to reason why, just invert and multiply'' that, for most students, meaninglessly enter one ear and leave the other.
To me, the most striking part was "yours is not to reason why". If that's how they taught, such practice should have been abandoned immediately. Or was it just an innocent piece of school folklore?
I launched a brief investigation (I believe, it was two years ago), and my findings were even more striking. Many people were asking why invert and multiply. Many people were answering, and the answers were quite unsatisfactory. Moreover, some people were asking where did the line came from - probably, because it was distorted - and I did not see any such question answered.
We do not learn all the time.
I have little sympathy to parents complaining about schools being too demanding. One of such complaints is that schools teach too fast. Like, every child learns at his or her own pace (which means, mine has a right to learn slow), etc.
Even before the recent dumbing down, schools were teaching too little and too slowly. And you know what, there is not much value in knowing that everybody else knows anyway. Let's leave the school alone and teach on our own. My only real complaint has always been that schools waste so much students' time just to keep their staff employed, and they are always hungry for more.
The notion of slow learning probably has to do with one-time programming. Kids get loaded with knowledge at school, and use it for the rest of their lives. Do I have to say that this is simply not so? Fighting for the student's right to be a slow learner the parents risk to leave she or he permanently falling behind. School actually tries to take care of those who are not catching up. The life does not.
There is another aspect though. It's well familiar to those who understand control, and practically unknown to many others. Once I noticed that my student was living through circles, or waves. A period of intellectual activity was followed by a "vegetative state", so to speak. This ups and downs were pronounced enough to disrupt learning, but I don't think they would qualify for cyclothymia. Even if they would, cyclothymia, like most of such "conditions", is nothing but a money sucker. We just got to learn to live in ourselves. I did.
It looks to me that school doesn't take such things into account. Returning to the previously taught topics, they assume that they have been learned. They just want to refresh the student's memory. In high school they mostly do it to prepare for the test (well, all their teaching is a preparation to the tests). Unfortunately, a "vegetative" period is more or less like a blackout. Given the cumulative nature of the teaching and the inevitable frustrations, this alone can make a good student bad.
The parents who teach their kids can discover the cycles (keeping records is essential) and take measures to prevent derailing at school. They just need to understand what's going on.
Here is another scenario. TLG wanted a pet. After understandable resistance, her mom suggested a bird. TLG was swept away. She was talking about birds, daydreaming, reading books, watching movies, and in the end of this period - which was rather short - I found that she completely forgot everything I taught her in the last couple months. Well, educations is as much about forgetting as it is about remembering, but imagine this happening while your child is attending school and supposed to be learning.
You told me what's going on.
Between the first and the second catastrophe, I was learning too. The teacher told me there was no textbook - I started reading homework sheets, apparently copied from a book, and it was one and the same book every time.
I have never attended American school. I had to look up too many words. Well, they were sort of teaching numeracy, except they were not teaching it. They were circling around endlessly. Some novelties came from discrete math and adjacent areas rather familiar to me. I would have appreciated this, but again, they were rather touching than teaching. Many things were weird, many others were silly. I straggled to get the meaning of "number sentence" - turned out, it had no meaning at all. They probably just wanted to make transition to algebra even harder. "Number sense" was (and still is) the biggest mystery. I suspect, it's extrasensory.
I commented on "math facts" in SHNUMBERS, did I? I understood it's actually a message. We don't want you to mess with your fingers. Remember simple additions, like there is no way to find them. Why lie about facts then? Just tell the students they got to memorize those additions by rote. Or would it undermine the image of reform math?
Lie was everywhere, and they called it math. I learned about reform math from Wikipedia. It was said to be different from good old math because the later was about computational algorithms, and the former was standard-based. OK, so why would not you include computational algorithms in your standards? You guys are just trying to sell something.
While writing this, I checked with Wikipedia one more time. The current explanation was not much different: a sales pitch, composed of scientifically looking words.
At some lucky moment, through AN OPEN LETTER TO UNITED STATES SECRETARY OF EDUCATION, RICHARD RILEY, I learned about Steven Leinwand's article in Education Week of 2/9/1994 and downloaded it. Instantly, everything started making sense. I realized I was struggling to understand a failed educational system.
I could have become a math hater. What a thought!
If you thought that my experience with two kids was not nearly enough to draw such conclusions, you are not getting me. I am not here to criticize US education or better it. I was just playing the game of my life, collecting the facts, deliberating, producing hypothesis and, most importantly, deciding what to do next. With my first American child I was afraid to do anything. I let his country raise him us much as I could. I could not teach him English. Not even baseball. I accepted the fact that I was good for nothing, and hoped that modern, advanced, professional and well-funded US school would compensate him for my failure to be an American dad.
I was more prepared and proactive with my second child. Still I missed the early signs, because I was not expecting another occurrence of the same problem. There was one important distinction: the boy was cocky, the girl was seriously scared, and this made me mad. When I realized that school did it again, I interfered very aggressively. I have no way to prove that it was me who turned the tide - you need statistics to make such claims - but the outcome was good.
I had one more child to waste or spare. She was three years old. Did I have to wait and see? I preferred to act, assuming, that US school was a factory of mathematical disabilities.
I had a powerful reason to believe it was. As I was piecing together their teaching, I realized I hated it. And then: being exposed to it slowly, day by day, I almost certainly would have become a math hater. I've never liked being taught this way.
The kids don't need numeracy any more? OK, teach them something equally or more challenging. Those who failed to understand multiplication, what can they learn at all? The hallmarks of reform math: "written and verbal communication, working in cooperative groups, making connections between concepts, and connections between representations" (quoted from Wikipedia) is simply not math, and not a substitute for it. Or "students' discovering their own knowledge and conceptual thinking" - come on, how much math, and especially conceptual thinking, can they discover on their own? Discovering such things, by the way, is not a knowledge at all. Like many pieces of reform math, it's a government-sponsored and enforced belief.
Most importantly, why do I have to assume that my kids are hopeless and allow teachers to scare them off mathematics? If school does not give them a chance to learn, I will. Who else?
Can it be be this bad?
Just six years ago, if I read that school can be perilous or evil, I would have thought that the writer was a conspiracy freak. Granted, I did not idealize school since I was 12 years old. Both my parents worked at school. More exactly, mom had always been a teacher and a deputy principal. Dad was trained as a teacher, and I am sure he was considering teaching to be a holy mission at first. He was instantly made a school principal - guess, just for being a male. Yet he deserted this trade at the earliest opportunity. For the rest of his life he was humorously bitter about education and it's servants, and he was not the only such humorist I was listening to.
I would agree that school was not exactly a pinnacle of intellectuality and no moral authority. I would admit that it could be harmful, just like about everything in real life. No doubt, it could have been damaging for some, who often had their parents and themselves to blame - again, like practically every other social establishment. This implied that school was not to be taken as seriously and trusted as deeply as it wanted. Loving it would be deeply immoral. However, a notion that parents should defend their kids from school I would have rebuked as a gross exaggeration.
The beginning of the story is in SHNUMBERS. When my first child went to the first grade and by the end of it became a proud American math hater, I could not exclude that he actually was one of them.
I was not prepared. Based on my previous experience, I hoped that he would "improve". No, he was getting worse. By the time I started systematic home schooling, he was probably hopeless. It was not just math, but rather his attitude to teachers and parents alike. He was certain that a smart guy like him would never need this brain-wrenching stuff.
I tried to talk to school workers. Some were kind enough to write a number of emails. They were pretty lucid. Like, you know what, we are entrusted by the Government to hold your kids for 8 hours a day 5 days a week, administering carefully selected and thoroughly vetted scientific methods. If your child failed to respond, go look for a doctor.
Teaching the boy mathematics, I was finding him perfectly able to learn. So did "developmentalists". Yet every time I approached school math, I saw a different person.
Immediately after his little sister had suffered and failed the first grade math, I grabbed her and in some 20 Summer hours taught her long positional addition, once and forever. It helped. I could do it, and I did it before, but not in the US. I was seriously wondering if Americans were born mathblind. I was wrong. Mine were disabled at school.