I don't offer live buttons because I promised not to expose my visitors to surveillance through third-party scripting. To share a link, please click to select one. As it turned blue, right-click on it and pick "Copy" from the browser's menu. To insert the copied link wherever your like, right-click again and pick "Paste" from the browser's menu.
Close this link selector..
Only parent can teach.
In the beginning of this blog, I told how my first two American kids became math haters at schools. I failed to help the first one, and it hurts. When education kicked the second one off track, I managed to put her back. By the end of the fourth grade, she was the best in class. She brought home the "gold seal" for "educational excellence", which I did not want at all. Good thing though, she is not miserable at school any more.
I am working with my third and, probably, the last child to prevent another disaster.
DEFENSIVE MATH was a reluctant offspring of my two other projects: MAKE THEM MAD and SHNUMBERS. What started as early teaching and remediation, grew into defense. At first, I thought it could become a book. Currently, I am converting it to a blog.I admit many chapters here are not sufficiently simple and detailed, but it's not a product yet. It only gives some idea what the first part of DEFENSIVE MATH could be like, if I'll get to finish it.
To call Table of Contents from anywhere at any time or to close it, please use the TOC control in the top-right corner. Thank you!
Next to the TOC there is the SHARE control. Click on it it to get the social media links.
The SIX opens the SIX PROJECTS web site. The DEFENSIVE MATH is one of them. Follow this link to find my email address.
The STEREO is the link to the online presentation STEREO LEARNING. It demonstrates how the projects work together to make STEM subjects learnable and their students teachable.
When I mentioned sticks and stakes in MINUS, MINUS, MINUS-MINUS, I knew I had to write an article about them. Mostly, to explain them better, but also to provide an entry point because they are very useful. This said, please, read the old chapter first.
To numeralize space, we tile the distances with a smaller distance called unit of measurement, and we count the tilings. The actual unit can be only one. We can move it forward, applying its beginning to where its end was.
While doing this, we count in one of two ways. First, we can count the units - the measuring sticks - like I did below.
This is what I call the stick model. It works best, if we can view the whole scene of measurement at once. This means, we must be big enough or soar high above to see the beginnings and the ends of the sticks.
Another way to count emerges where the distances are big, and we are small. The first example of it could have been the milestones of Ancient Rome. Numbering the middles of the miles would not be very practical. The milestones marked the beginnings and the ends of the miles. Standing at a milestone, the travelers knew how far away from Rome they were. I imagine a measuring rope with two stakes. The holes left where the stakes were stuck in the ground are points, and we count them. That's what I call the stake model of distance.
I don't supply the picture for the stake model. It's just a number line. I drew plenty of them for MINUS, MINUS, MINUS-MINUS.
On a small scale, the stake model is awfully problematic because we see too much. Counting the distances from zero, kids must exclude the zero point. For those who are not trained in sticks and stakes, zero is a point like any other. Why don't we count it then? Because zero is nothing? OK, but if we count through zero, we count zero point and exclude some other point, at which we begin.
On a line, we always have one extra point. If we join the endpoints of a line segment to make a contour, they become a single point. Think about a clock face. Oh, no, don't think about a clock face. The English AM/PM system is insane.
The intuition behind the sticks is much more solid. Fortunately, the pieces of paper, on which teachers offer their problems, are always smaller than the students, so the stick model is the best. Like probably every parent, I tell my kids to convert stakes to sticks. If in doubt, draw arcs and count them.
I can imagine an overly smart child drawing arcs between the middles of the sticks and counting them. The rule was explained in MINUS, MINUS, MINUS-MINUS: only distances count. It's a metric space.
In the stick model, there is no zero stick. Zero means no sticks. There was no zero in Ancient Rome too, but they did have so-called Golden Milestone, from which every road was supposed to be measured.
A good method to make stakes palatable involves another heresy: a unary operation of increment. Vitruvius described (but not invented) an odometer, a wheel-based mechanism dropping a pebble preloaded in a hole once a mile. In Ancient Rome, they called pebbles calculi, so the distances could be calculated.
Starting from empty (which was exactly 0), the system would increment the number of the calculi in the receiving compartment. One thought of such a machine running along the number line must be enough to answer every question and obliterate any doubt. Anybody knows where to buy a cheap plastic rendition by any chance? OK then, teach to use increment rather than addition. It's even cheaper.
Drawing one-dimensional sticks and stakes, we have an extra dimension for numbers and letters. In two dimensions, sticks become squares, and we can place our marks inside them. Such squares are handy for measuring areas.
Two-dimensional stakes remain points, and we often use grids to highlight their spatial order. The third dimension is not readily available for drawing. This tempts us to draw points (stakes) as squares (sticks).
A chart of addition on this animated page from STEREOLEARNING is made out of squares. The numbers are inside them. The chart looks like a stick model, but it isn't. Invisible stakes are in the centers of the squares. Zero is in place, and a navigator must skip the first number when counting.
Such transformations are frequent and difficult to understand. Many tables have their actual grids passing through the cells and intersecting inside them.
We must specifically train our kids to understand sticks and stakes. Allow me to give you one more reason why: The chart of multiplication available through this link is a stick model. There is no zero, and we count from the first number.
I don't explicitely teach TLG sticks and stakes yet, but I point out the differences and explain them. From time to time I even offer her problems. Occasionally, I still see her making mistakes trying to use a times table as an addition table.
A proven way to make them very mad.
The shnumber on the board is equal to -30814. How? I made it out of holes, or empty spaces, and turned upside down.
Telling such shnumber is relatively easy. Making operations with holes requires silencing your intuition and following the rules. This is quintessential for mathematics. Just try.
Besides being a brain twister, such shnumbers are models of negative quantities. Male elements are ones, female elements are minus ones (please excuse me for being an electronics engineer). When the hole is filled, it becomes zero.
This model once made TLG's little sister very frustrated. I did not offer it to TLG yet.
Putting a positive board on top of a negative board, we can add up negative and positive quantities. Fortunately, there are other ways to do it, because filling boards with pegs is taxing. Unfortunately, I can't offer or recommend a computer program for such manipulations. You can drag and snap circles using any free object-oriented editor, don't even think of letting kids do it though, because of the presence of the shape-changing controls.
Remark that adding a positive number to a negative number you perform subtraction (with "borrowing"), but nothing prevents you from subtracting bigger number from smaller number. You simply end up with unfilled holes.
Making connections between representations
In SHNUMBERS, I disclosed that I am an oversimplificator. I am simply not smart enough to understand and appreciate the subjects like reform math. To me this reform means that teachers got science off their backs, and happily allowed themselves not to teach. The school is now free, and nothing in this democracy can bring it under control.
I wish it was so simple. In reality, school keeps itself employed imitating teaching. It looks like they throw at the students everything in hope something may stick (guess, that's how they understand the multiple embodiment principle). Knowing arithmetic is no longer enough, and, actually, is not even required. The students got to learn the silly stuff, call it common core or whatever. Or else.
"Standards" (another name for silly stuff meant to keep teachers busy) can be good for bad students. They may not know how to multiply, but if they learned to look up the data in the linear tables or recognize the patterns like 13579, this would be something.
School operates under an assumption that a standard American student can not learn multiplication. I don't believe in this, but I have something else to care. What if my children can? School make them learn as if they could not, or punish. Trust an immigrant, who can't even speak decent English: teachers still think that they are surrounded with cavemen, and believe they are the ones who carry the torch.
Even for the teachers, picking and getting the silly stuff falling from above is hard. The best defense I can think of as a parent is: aim high. Teach representations that may knock the reformers' socks off.
Here is a recent example. I have a plastic jar with 1000 1 cm cubes, like the ones in Dienes sets. We don't open it often. The cubes are too small, poorly made, and the colors are ugly.
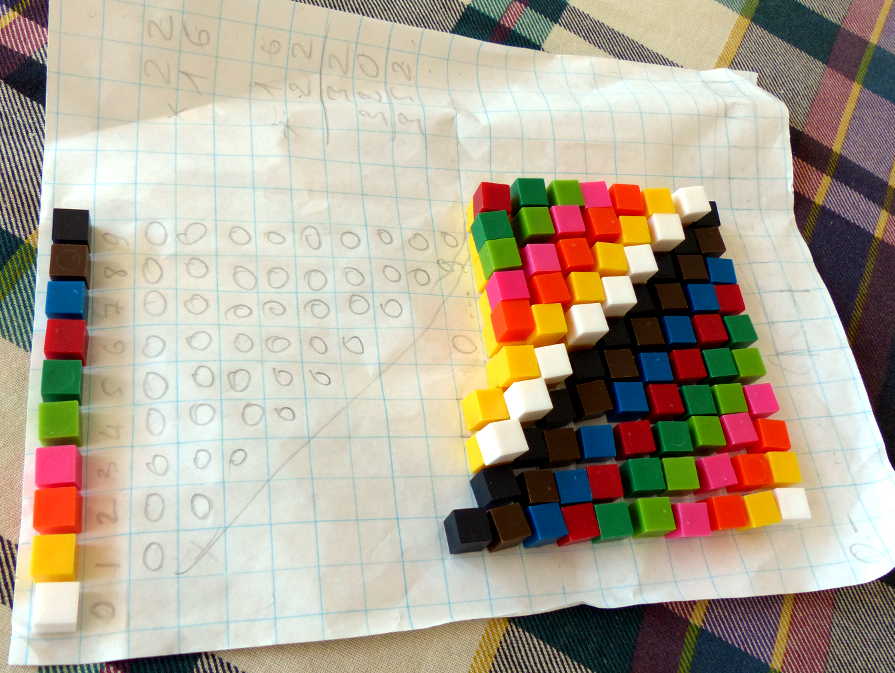
Suddenly, I realized that there were 10 colors in the set. I built the table linking them to numerals and suggested to perform computations in colors. This did not make TLG happy - she hates everything new - but she quickly got the idea. By the following lesson she remembered them all (I did not) and called the colors by their numeral names quite confidently.
I challenged TLG to build the chart of additions in color. She agreed, but I had to do the gluing. Otherwise she wold probably get mad at me because the idea became too simple to her to be exciting.
So TLG was telling me which color to glue next, and we ended up with what you see on the picture. We could not finish it because I ran out of glue dots, but the progress was convincing enough.
Teaching at home, I present new concepts from different angles or try to derive them from what TLG has learned before (not necessarily in mathematics), but it's not multiple embodiments. Even at it's finest, the idea of multiple embodiment contradict all my learning and teaching experience. I believe the abstract ideas must be acquired on some familiar substrate (I use pegboards a lot). TLG's intellectual life has been revolving around those awful pegboards since she was 2 years and 4 months old.
This said, there is a similar problem, which American school with it's dependence on formal testing greatly amplifies. Once kids learn notation, they quickly forget what it means. They may know how to use it, but in the core their knowledge is absurd. I am constantly trying to break the ice, offering new disguises for well studied concepts. In the language of reform math, I want them to make connections between concepts and representation.
Tracking invisible quantity
Please allow me one more quote from Wikipedia. It's not supposed to be an authoritative source, but you know what Wikipedia really is.
The American Institutes for Research (AIR) reported in 2005 that the NCTM proposals "risk exposing students to unrealistically advanced mathematics content in the early grades."[14] This is in reference to NCTM's recommendation that algebraic concepts, such as understanding patterns and properties like commutativity (2+3=3+2), should be taught as early as first grade.
This is sad, but again, I am not in charge of "most students". TLG knows and uses commutativity since she learned addition, and she learned long addition before she turned five. Putting a bigger number first, always makes computation easier. Associativity? Adding something like 1+7+9, she applies 1 to 9. There is no positional arithmetic without algebra. And let me remind you what a regular minority kid could do with patterns.
TLG can use formulas. Absolutely. The notion that young kids can't learn such things is either ignorance or deliberate manipulation. Big kids, who underwent many years of brain stiffening treatment at school, do have troubles learning to use names and roles for numbers. Small kids, who learn naming things, don't.
When TLG's faint-hearted big sister was learning positional addition on shnumbers, I explained to her elementary algebra using letters for colors. R is the red quantity, B is the blue. It was perfectly fine. Several months later my suggestion to use letters for numbers made her upset. I reminded her she did it with pegs. She recalled this, but now she knew that letters were pre-algebra, and pre-algebra was to be afraid of. I believe, that's how I've heard about pre-algebra for the first time.
In the beginning of the forth grade, she mentioned that next year she would start pre-algebra and said she was scared of it. I assured her that she already knew this silly subject, and taught her recurrence relations.
While I was teaching TLG's big sister, the other kids, or, maybe, even teachers (the art teacher, quite probably), were telling her horror stories. That's how school controls the population.
Between TLG's fourth and fifth birthdays (closer to the fourth) I took a plain paper bag and crossed it corner to corner with red marker. This device came to be known as X-bag. Another one was Y-bag. At first I was stuffing the bags with counting bears, and TLG was keeping tracks of my additions. Then I started asking questions like: if I put 3 more bears in the bag, there will be 8 of them. What the mystery number X is equal to?
TLG quickly understood equations and she solves them - guess, for the time being her method is good enough because she is still learning how addition and subtraction work together. By the way, she learned about negative numbers and zero from her mom before she turned 4, and her understanding is very solid. I tried to catch her many times.
Recently, I returned X and Y bags on stage. TLG remembered them, and was happy to see them again. We moved some pegs back and forth carefully watching and tracking the matching additions and subtractions as they occurred. Next we moved paper cards with big numbers.
She is just a little girl.
I introduced TLG (The Little Girl) in MAKE THEM MAD, and even "shared" two pictures of her taken when she was much younger. She does not look nearly like this. She is six years old, and she just started her kindergarten year.
I am still homeschooling TLG. My goal is to teach her numeracy, not leaving reform math any chance. She just started doing long subtraction (10 digits and more), she knows all the operations (and she even understands they are operations) and she got many gifts from pre-algebra treasure chest. Or, maybe, algebra. I don't care what they teach any more.According to its proponents, reform math was supposed to be a blessing for women and minorities. TLG is a girl. She is an offsprings of a pretty poor minority (and a very small minority, as a matter of fact). Yet it does not look like she belongs to "most students" of Steven Leinwand's article.
On average, our lesson takes 30 minutes per day, and it's not only numbers. I would much prefer to do something else, but we can't afford much of it. TLG just told me, pointing at her forehead, that she constantly reminds herself not to hate math after the first grade. I only mentioned it, maybe, couple times, when she did not want to learn.
Otherwise TLG is a normal American girl, and her interests are normal for this part of the population too, except she is more advanced than her peers in every aspect. It's not my words, it's official. Fortunately, the officials have no idea how advanced, and, most importantly, how different she is. They prefer to be professionally blindsided. As for TLG, I am telling her that truly smart people do not show how smart they are.
Which I prefer to call reciprocation.
Multiplication is repeated addition. Division is repeated subtraction. We can always multiply two integer numbers. Occasionally, we can also divide one number by another one and get yet another integer number.
To make division always possible, we need rational numbers. Rational numbers are combinations of integer number and fractions. Once we admitted them to the scene, we understood that every integer number can produce a pair of rational numbers: We only need to divide it by one and divide one by it. Where we had 9, we now have 9/1 and 1/9.
Remember the meaning of the words numerator and denominator: 9/1 means nine of ones. Like any number, 9 is just a bunch of 1s.
This brings about another unary operation of inversion, which I like to call reciprocation. It turns 1/N to N/1 and back.
Forget fractions, what do you do to divide by a whole number? You reciprocate it, so that 9/1 becomes 1/9, and multiply. Dealing with any other rational number, you just do the same.
The first inversion - the one turning negative to positive and positive to negative - could be understood as subtraction from 0 or multiplication by -1. Reciprocation of a number can be understood as division of 1 by this number or as power -1 of this number.
School shows mathematical machine wiggling its limbs. Make the cover transparent. Let kids see how it works.
Kids know them, teachers don't.
From different students of different elementary schools, I heard that many in their classes knew about negative numbers, yet the teachers were telling them that it is not possible to subtract a bigger number from a smaller one.
If your student is smart enough to understand negative numbers, why would not you try to perform a forbidden subtraction? What, for example, is 203-447? I am not sure how exactly they do subtraction in reformed US schools, so I tried to make it very clear.
The first line on the illustration has position numbers. The blackened and underlined position is where we are. Click on FORTH and watch. When you reached #3, please remember that spaces in front of a positional number (as well as behind it) is, in fact, the infinite line of zeros. Without them even addition would not be possible.
Remark that FORTH is on the left from BACK. That's because we Europeans have borrowed positional numeral system from Arabs together with their writing order.After #5 the demonstration ends. Clearly, we can go like this forever. I put … in front 9 to indicate that the infinite line of 0s became the infinite line of 9s. Few extra 9s were for clarity. …9 or …0 would (and will) be enough.
The infinite line of 9s looks scary, but no scarier than a periodic fraction. I decide not to use any special mark (like vinculum on top of a periodic part). For this demo an ellipsis before 9 is good enough.
We could do subtraction in strict accordance with the rules, and we can do it for any other two numbers, putting the smaller one first, but what's the use of those forever nine numerical freaks?
Let's try to add 447 to …9756. Here is how.
Going like this forever, we will get …0203, or just 203. Remark that it was not subtraction. Just plain addition. Is …9756 secretly equal to -244?
It's no different. Try do add it to some other numbers, big and small, to make sure that we found a perfectly workable representation of negative quantity, which eliminates subtraction entirely.
Wait a moment, how about number sense? An infinite line of 9s looks like an awful lot!
No matter how it looks, the biggest whole positional number …9 (an infinitely big whole number made entirely of nines) is just one smaller that 0. Try to add 1 to …9. It becomes 0. This can only mean that …9=-1 (…9.9…, which is infinite 9 to the left and infinite 9 to the right from the decimal point, is infinitely approaching 0).
This means, in turn, that our familiar number line is actually an infinitely wide circle. The biggest number we can think of approaches 0 from the other side.
Remark though, that this observation is not about quantity or geometry. It's about positional numeral system. It would not make much sense, for example, to ask infinitely deep questions like will the wave of additions will ever catch up with the wave of subtractions. Once they traveled out of view and far enough, we can use the visible part like there is nothing to the left from it. After all, there are no infinite positional numbers in real life.
Just couple more paragraphs, OK? …90=-10, …900=-100 and so forth. The number …9756 is -1000+756=-244, precisely as expected. Or how about multiplication?
…9756+…9756+…9756=…9268
Please don't think that this chapter was a singular pointless bump on the smooth road to numeracy. If you got it, you will easily understand how machines, including computers, handle quantities. And I have more to tell.
I've never happened to teach negative numbers. Every student in my life, big or little, already knew them. The knowledge of infinity is not so common, but every kid was pretty comfortable learning it.
Not a sign, but an operation to change it.
Mathematics is so notoriously difficult to learn because education is so conservative and selfish. They teach like many hundreds years progress never happened. They squirrel away every helpful invention and discovery and turn it into an obstacle to learning. Mathematics, which is tremendously useful and empowering, they present as a scare.Without introducing anything new, let's just rewire the teaching. I will use a simple and exciting narrative: people were inventing new operations, they tried to reverse them, and every time this led to a discovery of a new kind of number.
The most basic operations are counting (increment) and counting back (decrement). Teaching them as such (like some preschool educators do) to me is simply impractical. Before you explain them to kids, they know numbers, so increment inevitably turns into +1. Still increment and decrement are very handy for teaching, and they allow us to introduce unary operations.
Incrementing many times at once is what we call addition. In positional system it's not just another name. We have a method, which makes addition much easier. Not even much easier, but exponentially easier. Demonstration of how positional addition is easier than counting forward is breathtaking (since I wrote this, I spent another month and produced STEREO LEARNING to illustrate some of such statements).
Repeated decrementing leads to subtraction, and we face the problem of numbers for the first time. We can always add two numbers. Incredibly, there alway is a natural number waiting to be discovered through addition. Yet we can not always perform subtraction. We need negative numbers to make it possible.
This kind of reasoning becomes available after we exposed our children to big numbers, which school does not do. Well, without big numbers you can only leave the learners to discover their knowledge and conceptual thinking. I keep picking on conceptual thinking because it's such a shameless lie. On par with calling a daycare an Academy.
As soon as we invented negative numbers, we understand that natural numbers - the only kind of numbers we knew before - are positive. Or we may think that every natural number can produce a pair of integer numbers if you add it to 0 and subtract from it.
Next comes another unary operation, which can be rightfully called inversion. I often call it negation, which is worse because of asymmetry. At school they do not teach such things. I wonder if Steven Leinwand knew that inversion is an operation.
Inversion turns negative numbers to positive and back. One way to do it is subtracting from 0. Another, and more interesting way, is multiplying by -1. In fact, -1 is the only negative number we need to build the rest of them.
The true meaning of the minus sign is the operation of inversion. Now what do you do to subtract a negative number? Yes. You invert and add.
Is it so easy? Of course it's not. Soon I will return to subtraction to discuss the problems with it. Elementary math is actually a toxic swamp. Allowing children to "discover" it without guidance is inhuman.
Theirs but to do and die
First thing first: the line came from this poem. At the Battle of Balaclava (no, not that balaclava, Balaclava is a town near Sevastopol in Crimea (yes, this Crimea)), which happened during Crimean War, a 600-strong British light cavalry detachment was sent to attack a powerful and well guarded Russian battery through so-called valley of Death. Apparently, due to their commander's mistake.
Next...
Theirs not to make reply,
Theirs not to reason why,
Theirs but to do and die:
Not all of them died, and those who did not, inspired another famous poem, but you better read the article.
What British cavalry was doing in Crimea is another story, and a very interesting one. Wikipedia has it too.
It took me years to realize that the "do and die" attitude was one of the biggest difficulties my wimpy kids were facing at schools. They were raised to understand. American school demanded blind obedience. I failed to prepare them for this.
Before answering why (invert and multiply), let me tell you that this must be the second inversion to learn. The first is invert and add.
Just invert and multiply
The name of Steven Leinwand's article was "It's Time To Abandon Computational Algorithms". He explained what exactly had to be abandoned in the following words.
...the formal, paper-and-pencil computational algorithms that constitute the core grade-school mathematical experiences of most American youngsters. It's about mindless procedures like "carrying threes into the tens column,'' "six times seven is 42, put down two and carry the four,'' and "eight from two, can't do, cross out the five, make it a four, and borrow 10.'' It's also about memorized rules like "yours is not to reason why, just invert and multiply'' that, for most students, meaninglessly enter one ear and leave the other.
To me, the most striking part was "yours is not to reason why". If that's how they taught, such practice should have been abandoned immediately. Or was it just an innocent piece of school folklore?
I launched a brief investigation (I believe, it was two years ago), and my findings were even more striking. Many people were asking why invert and multiply. Many people were answering, and the answers were quite unsatisfactory. Moreover, some people were asking where did the line came from - probably, because it was distorted - and I did not see any such question answered.
We do not learn all the time.
I have little sympathy to parents complaining about schools being too demanding. One of such complaints is that schools teach too fast. Like, every child learns at his or her own pace (which means, mine has a right to learn slow), etc.
Even before the recent dumbing down, schools were teaching too little and too slowly. And you know what, there is not much value in knowing that everybody else knows anyway. Let's leave the school alone and teach on our own. My only real complaint has always been that schools waste so much students' time just to keep their staff employed, and they are always hungry for more.
The notion of slow learning probably has to do with one-time programming. Kids get loaded with knowledge at school, and use it for the rest of their lives. Do I have to say that this is simply not so? Fighting for the student's right to be a slow learner the parents risk to leave she or he permanently falling behind. School actually tries to take care of those who are not catching up. The life does not.
There is another aspect though. It's well familiar to those who understand control, and practically unknown to many others. Once I noticed that my student was living through circles, or waves. A period of intellectual activity was followed by a "vegetative state", so to speak. This ups and downs were pronounced enough to disrupt learning, but I don't think they would qualify for cyclothymia. Even if they would, cyclothymia, like most of such "conditions", is nothing but a money sucker. We just got to learn to live in ourselves. I did.
It looks to me that school doesn't take such things into account. Returning to the previously taught topics, they assume that they have been learned. They just want to refresh the student's memory. In high school they mostly do it to prepare for the test (well, all their teaching is a preparation to the tests). Unfortunately, a "vegetative" period is more or less like a blackout. Given the cumulative nature of the teaching and the inevitable frustrations, this alone can make a good student bad.
The parents who teach their kids can discover the cycles (keeping records is essential) and take measures to prevent derailing at school. They just need to understand what's going on.
Here is another scenario. TLG wanted a pet. After understandable resistance, her mom suggested a bird. TLG was swept away. She was talking about birds, daydreaming, reading books, watching movies, and in the end of this period - which was rather short - I found that she completely forgot everything I taught her in the last couple months. Well, educations is as much about forgetting as it is about remembering, but imagine this happening while your child is attending school and supposed to be learning.
You told me what's going on.
Between the first and the second catastrophe, I was learning too. The teacher told me there was no textbook - I started reading homework sheets, apparently copied from a book, and it was one and the same book every time.
I have never attended American school. I had to look up too many words. Well, they were sort of teaching numeracy, except they were not teaching it. They were circling around endlessly. Some novelties came from discrete math and adjacent areas rather familiar to me. I would have appreciated this, but again, they were rather touching than teaching. Many things were weird, many others were silly. I straggled to get the meaning of "number sentence" - turned out, it had no meaning at all. They probably just wanted to make transition to algebra even harder. "Number sense" was (and still is) the biggest mystery. I suspect, it's extrasensory.
I commented on "math facts" in SHNUMBERS, did I? I understood it's actually a message. We don't want you to mess with your fingers. Remember simple additions, like there is no way to find them. Why lie about facts then? Just tell the students they got to memorize those additions by rote. Or would it undermine the image of reform math?
Lie was everywhere, and they called it math. I learned about reform math from Wikipedia. It was said to be different from good old math because the later was about computational algorithms, and the former was standard-based. OK, so why would not you include computational algorithms in your standards? You guys are just trying to sell something.
While writing this, I checked with Wikipedia one more time. The current explanation was not much different: a sales pitch, composed of scientifically looking words.
At some lucky moment, through AN OPEN LETTER TO UNITED STATES SECRETARY OF EDUCATION, RICHARD RILEY, I learned about Steven Leinwand's article in Education Week of 2/9/1994 and downloaded it. Instantly, everything started making sense. I realized I was struggling to understand a failed educational system.
I could have become a math hater. What a thought!
If you thought that my experience with two kids was not nearly enough to draw such conclusions, you are not getting me. I am not here to criticize US education or better it. I was just playing the game of my life, collecting the facts, deliberating, producing hypothesis and, most importantly, deciding what to do next. With my first American child I was afraid to do anything. I let his country raise him us much as I could. I could not teach him English. Not even baseball. I accepted the fact that I was good for nothing, and hoped that modern, advanced, professional and well-funded US school would compensate him for my failure to be an American dad.
I was more prepared and proactive with my second child. Still I missed the early signs, because I was not expecting another occurrence of the same problem. There was one important distinction: the boy was cocky, the girl was seriously scared, and this made me mad. When I realized that school did it again, I interfered very aggressively. I have no way to prove that it was me who turned the tide - you need statistics to make such claims - but the outcome was good.
I had one more child to waste or spare. She was three years old. Did I have to wait and see? I preferred to act, assuming, that US school was a factory of mathematical disabilities.
I had a powerful reason to believe it was. As I was piecing together their teaching, I realized I hated it. And then: being exposed to it slowly, day by day, I almost certainly would have become a math hater. I've never liked being taught this way.
The kids don't need numeracy any more? OK, teach them something equally or more challenging. Those who failed to understand multiplication, what can they learn at all? The hallmarks of reform math: "written and verbal communication, working in cooperative groups, making connections between concepts, and connections between representations" (quoted from Wikipedia) is simply not math, and not a substitute for it. Or "students' discovering their own knowledge and conceptual thinking" - come on, how much math, and especially conceptual thinking, can they discover on their own? Discovering such things, by the way, is not a knowledge at all. Like many pieces of reform math, it's a government-sponsored and enforced belief.
Most importantly, why do I have to assume that my kids are hopeless and allow teachers to scare them off mathematics? If school does not give them a chance to learn, I will. Who else?
Can it be be this bad?
Just six years ago, if I read that school can be perilous or evil, I would have thought that the writer was a conspiracy freak. Granted, I did not idealize school since I was 12 years old. Both my parents worked at school. More exactly, mom had always been a teacher and a deputy principal. Dad was trained as a teacher, and I am sure he was considering teaching to be a holy mission at first. He was instantly made a school principal - guess, just for being a male. Yet he deserted this trade at the earliest opportunity. For the rest of his life he was humorously bitter about education and it's servants, and he was not the only such humorist I was listening to.
I would agree that school was not exactly a pinnacle of intellectuality and no moral authority. I would admit that it could be harmful, just like about everything in real life. No doubt, it could have been damaging for some, who often had their parents and themselves to blame - again, like practically every other social establishment. This implied that school was not to be taken as seriously and trusted as deeply as it wanted. Loving it would be deeply immoral. However, a notion that parents should defend their kids from school I would have rebuked as a gross exaggeration.
The beginning of the story is in SHNUMBERS. When my first child went to the first grade and by the end of it became a proud American math hater, I could not exclude that he actually was one of them.
I was not prepared. Based on my previous experience, I hoped that he would "improve". No, he was getting worse. By the time I started systematic home schooling, he was probably hopeless. It was not just math, but rather his attitude to teachers and parents alike. He was certain that a smart guy like him would never need this brain-wrenching stuff.
I tried to talk to school workers. Some were kind enough to write a number of emails. They were pretty lucid. Like, you know what, we are entrusted by the Government to hold your kids for 8 hours a day 5 days a week, administering carefully selected and thoroughly vetted scientific methods. If your child failed to respond, go look for a doctor.
Teaching the boy mathematics, I was finding him perfectly able to learn. So did "developmentalists". Yet every time I approached school math, I saw a different person.
Immediately after his little sister had suffered and failed the first grade math, I grabbed her and in some 20 Summer hours taught her long positional addition, once and forever. It helped. I could do it, and I did it before, but not in the US. I was seriously wondering if Americans were born mathblind. I was wrong. Mine were disabled at school.